Question

【题目】如图，已知三棱柱BCF﹣ADE的侧面CFED与ABFE都是边长为1的正方形，M、N两点分别在AF和CE上，且AM=EN．
（1）求证：平面ABCD⊥平面ADE；
（2）求证：MN∥平面BCF；
（3）若点N为EC的中点，点P为EF上的动点，试求PA+PN的最小值．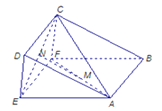

Answer 1

【答案】解：（1）∵四边形CFED与ABFE都是正方形
∴EF⊥DE，EF⊥AE，又DE∩EA=E，∴EF⊥平面ADE，
又∵EF∥AB，∴AB⊥平面ADE
∵AB平面ABCD，∴平面ABCD⊥平面ADE
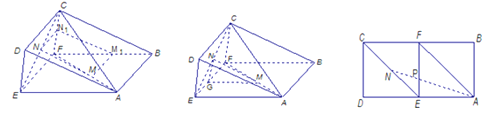
（2）证法一：过点M作MM1⊥BF交BF于M1 ，
过点N作NN1⊥CF交BF于N1 ， 连结M1N1 ，
∵MM1∥AB，NN1∥EF∴MM1∥NN1
又∵，
∴MM1=NN1
∴四边形MNN1M1为平行四边形，
∴MN∥N1M1 ， 又MN面BCF，N1M1面BCF，∴MN∥面BCF．
[法二：过点M作MG⊥EF交EF于G，连结NG，则，∴NG∥CF
又NG面BCF，CF面BCF，∴NG∥面BCF，
同理可证得MG∥面BCF，又MG∩NG=G，∴平面MNG∥平面BCF
∵MN平面MNG，∴MN∥面BCF．
（3）如图将平面EFCD绕EF旋转到与ABFE在同一平面内，则当点
A、P、N在同一直线上时，PA+PN最小，
在△AEN中，∵
由余弦定理得AN2=AE2+EN2﹣2AEENcos135°，
∴AN=，
即．

【解析】（1）四边形CFED与ABFE都是正方形，利用线面垂直可得EF⊥平面ADE，再根据EF∥AB，得出AB⊥平面ADE，最后利用面面垂直的判定得出结论；
（2）证法一：过点M作MM1⊥BF交BF于M1 ， 过点N作NN1⊥CF交BF于N1 ， 连结M1N1 ， 先证得四边形MNN1M1为平行四边形，得MN∥N1M1 ， 再根据线面平行的判定得到MN∥面BCF．
法二：过点M作MG⊥EF交EF于G，连结NG，得出平面MNG∥平面BCF，最后利用面面平行的性质得出MN∥面BCF；
（3）将平面EFCD绕EF旋转到与ABFE在同一平面内，则当点A、P、N在同一直线上时，PA+PN最小．通过解△AEN，利用余弦定理求出AN即可。
【考点精析】本题主要考查了直线与平面平行的判定和平面与平面垂直的判定的相关知识点，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；一个平面过另一个平面的垂线，则这两个平面垂直才能正确解答此题．