Question

【题目】某厂为检验车间一生产线是否工作正常，现从生产线中随机抽取一批零件样本，测量尺寸（单位： mm ）绘成频率分布直方图如图所示：

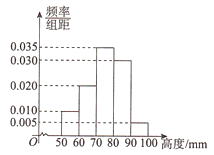
（Ⅰ）求该批零件样本尺寸的平均数 x 和样本方差 （同一组中的数据用该组区间的中点值作代表）；

（Ⅱ）若该批零件尺寸 服从正态分布 ，其中 近似为样本平均数 近似为样本方差 ，利用该正态分布求 ；

（Ⅲ）若从生产线中任取一零件，测量尺寸为30mm，根据 原则判断该生产线是否正常？

附： ；若，则 ， ， .

Answer 1

【答案】(1)75；110.

(2)0.8185.

(3) 该生产线工作不正常.

【解析】试题分析：

(Ⅰ)由题意结合频率分布直方图计算可得该批零件样本尺寸的平均数，样本方差.

(Ⅱ)由（Ⅰ）知，，则正态分布的对称轴为，结合正态分布图象的对称性和准则可得 .

(Ⅲ)由题意可知，而，故该生产线工作不正常.

试题解析：

（Ⅰ） .

；

（Ⅱ）由（Ⅰ）知，.

从而 ，

，

∴ .

（Ⅲ）∵，，

∴.

∵，小概率事件发生了，

∴该生产线工作不正常.