题目内容
【题目】定义在
上的偶函数
满足
，当
时，
，设函数
，则与
的图象所有交点的横坐标之和为（ ）．
A. 3B. 4C. 5D. 6
【答案】B
【解析】
由函数图象的性质得：f（x）的图象关于直线x＝1对称且关于y轴对称，函数g（x）＝e﹣|x﹣1|（﹣1＜x＜3）的图象也关于直线x＝1对称，由函数图象的作法可知两个图象有四个交点，且两两关于直线x＝1对称，则f（x）与g（x）的图象所有交点的横坐标之和为4，得解
由偶函数f（x）满足 （1+x）＝f （1﹣x）可得f（x）的图象关于直线x＝1对称且关于y轴对称，
函数g（x）＝e﹣|x﹣1|（﹣1＜x＜3）的图象也关于直线x＝1对称，
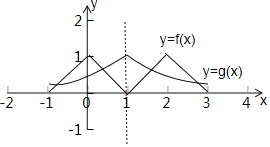
函数y＝f（x）的图象与函数g（x）＝e﹣|x﹣1|（﹣1＜x＜3）的图象的位置关系如图所示，
可知两个图象有四个交点，且两两关于直线x＝1对称，
则f（x）与g（x）的图象所有交点的横坐标之和为4，
故选：B．
练习册系列答案
相关题目
