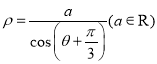题目内容
【题目】如图,椭圆![]() 的离心率
的离心率![]() ,且椭圆C的短轴长为
,且椭圆C的短轴长为![]() .
.
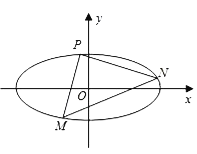
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 椭圆
椭圆![]() 上的三个动点.
上的三个动点.
(i)若直线![]() 过点D
过点D![]() ,且
,且![]() 点是椭圆
点是椭圆![]() 的上顶点,求
的上顶点,求![]() 面积的最大值;
面积的最大值;
(ii)试探究:是否存在![]() 是以
是以![]() 为中心的等边三角形,若存在,请给出证明;若不存在,请说明理由.
为中心的等边三角形,若存在,请给出证明;若不存在,请说明理由.
【答案】(1) 椭圆![]() 的方程是
的方程是![]()
![]()
![]() 面积的最大值为
面积的最大值为![]()
![]() 不存在
不存在![]() 是以
是以![]() 为中心的等边三角形.
为中心的等边三角形.
【解析】
![]() 利用离心率以及短轴长,求出椭圆中
利用离心率以及短轴长,求出椭圆中![]() .即可求椭圆
.即可求椭圆![]() 的方程;
的方程;
![]() 由已知,直线
由已知,直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 方程,联立直线与椭圆方程,利用韦达定理,弦长公式,推出面积的表达式,通过换元,利用导数求出面积的最大值.
方程,联立直线与椭圆方程,利用韦达定理,弦长公式,推出面积的表达式,通过换元,利用导数求出面积的最大值.
![]() 假设存在
假设存在![]() 是以
是以![]() 为中心的等边三角形.
为中心的等边三角形.
![]() 当
当![]() 在
在![]() 轴上时,推出与
轴上时,推出与![]() 为等边三角形矛盾.
为等边三角形矛盾.
![]() 当
当![]() 在
在![]() 轴上时,推出与
轴上时,推出与![]() 为等边三角形矛盾.
为等边三角形矛盾.
![]() 当
当![]() 不在坐标轴时,推出与
不在坐标轴时,推出与![]() 为等边三角形矛盾.故得解.
为等边三角形矛盾.故得解.
(1)由已知得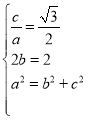 ,解得
,解得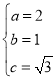 ,
,
所以椭圆![]() 的方程是
的方程是![]()
![]() 由已知可知直线
由已知可知直线![]() 的斜率定存在,设直线
的斜率定存在,设直线![]() 的方程为
的方程为![]() ,
,
![]() ,
,
由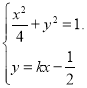 得
得![]() ,所以
,所以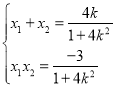
所以![]() ,
,
又![]() ,所以
,所以 ,
,
令![]() ,
,
所以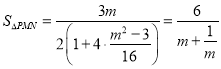 ,
,
令![]() ,则
,则![]()
所以![]() 在
在![]() 上单调递增,所以当
上单调递增,所以当![]() 时,此时
时,此时![]() ,
,![]() 有最小值
有最小值![]() 此时
此时![]() 有最大值
有最大值![]() .
.
故得解.
![]() 不存在
不存在![]() 是以
是以![]() 为中心的等边三角形.理由如下:
为中心的等边三角形.理由如下:
假设存在![]() 是以
是以![]() 为中心的等边三角形.
为中心的等边三角形.
![]() 当
当![]() 在
在![]() 轴上时,
轴上时,![]() 的坐标为
的坐标为![]() ,则
,则![]() 关于
关于![]() 轴对称,
轴对称,![]() 的中点
的中点![]() 在
在![]() 轴上.
轴上.
又![]() 为
为![]() 的中心,所以
的中心,所以![]() ,可知
,可知![]() ,
,
从而![]() ,即
,即![]() .
.
所以与![]() 为等边三角形矛盾.
为等边三角形矛盾.
![]() 当
当![]() 在
在![]() 轴上时,
轴上时,![]() 的坐标为
的坐标为![]() ,则
,则![]() 关于
关于![]() 轴对称,
轴对称,![]() 的中点
的中点![]() 在
在![]() 轴上.
轴上.
又![]() 为
为![]() 的中心,所以
的中心,所以![]() ,可知
,可知 ,
,
从而![]() ,即
,即![]() .
.
所以与![]() 为等边三角形矛盾.
为等边三角形矛盾.
![]() 当
当![]() 不在坐标轴时,设
不在坐标轴时,设![]() ,
,![]() 的中点为
的中点为![]() ,则
,则![]() ,
,
又![]() 为
为![]() 的中心,则
的中心,则![]() ,可知
,可知![]() .
.
设![]() ,则
,则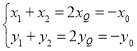 ,
,
又![]() ,两式相减得
,两式相减得![]() ,
,
从而![]()
![]() ,
,
所以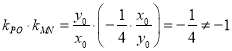 ,
,
所以![]() 与
与![]() 不垂直,与等边
不垂直,与等边![]() 矛盾.
矛盾.
综上所述,不存在![]() 是以
是以![]() 为中心的等边三角形.
为中心的等边三角形.

 53随堂测系列答案
53随堂测系列答案【题目】点P为两直线l1:3x+4y﹣2=0和l2:2x+y+2=0的交点.
(1)求过P点且与直线3x﹣2y+4=0平行的直线方程;
(2)求过原点且与直线l1和l2围成的三角形为直角三角形的直线方程.