Question

【题目】四棱锥底面是菱形，平面，，分别是的中点.

（1）求证：平面平面；

（2），垂足为，斜线与平面所成的角为，求二面角的正切值.

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）设菱形的边长为，由勾股定理推导出，，由线面垂直得到，由此能证明面.

（2）过作，垂足为，过作，垂足为，连，则是二面角的平面角，由此能求出二面角的正切值.

（1）证明：∵底面底面是菱形，

∴是正三角形

又为中点，∴，

故，即

∵平面，∴

又，∴平面

而在平面内，∴平面平面

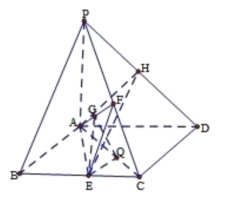
（2）解法一：由（1）知，平面，∴是与平面所成的角

∵，

过作于点，过作于点，连结

∵平面，∴

又，，∴平面

∵AF在平面PAC内，∴

又，，∴平面，进而

∴是二面角的平面角

设，则，

∵，∴，

∴，

∴在直角三角形中，，

又，∴是正三角形，

∴

∴