题目内容
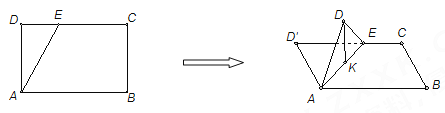
【题目】小明设计了一款正四棱锥形状的包装盒，如图所示，
是边长为
的正方形硬纸片，切去阴影部分所示的四个全等的等腰三角形，再沿虚线折起，使得四个点重合于图中的点
，正好形成一个正四棱锥形状的包装盒，设正四棱锥底面正方形的边长为
.
（1）试用表示该四棱锥的高度
，并指出的取值范围；
（2）若要求侧面积不小于
，求该四棱锥的高度的最大值，并指出此时该包装盒的容积.
【答案】（1）
；（2）
，
.
【解析】
（1）设正四棱锥侧面等腰三角形高为
，由正方形
，可得
，再由
组成直角三角形，即可得到
关系，进而求出
的范围；
（2）利用（1）中
关系，求出侧面积关于的函数，进一步求出满足条件的范围，可求出
的最大值，即可求出结论.
（1）设正四棱锥侧面等腰三角形高为，在正方形中，
，
在四棱锥中，
，
，
，
；
（2）四棱锥的侧面积
，
，解得
，
，当
时，
，
此时包装盒的容积为
，
所以满足条件的四棱锥的高度的最大值为20，
此时该包装盒的容积为.
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
