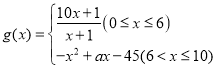Question

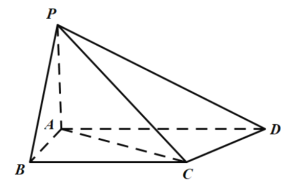
【题目】设正四面体ABCD的所有棱长都为1米，有一只蚂蚁从点A开始按以下规则前进：在每一个顶点处等可能地选择通过这个顶点的三条棱之一，并且沿着这条棱爬到尽头，则它爬了4米之后恰好位于顶点A的概率为（ ）

A.B.C.D.

Answer 1

【答案】A

【解析】

本题是一个等可能事件的概率，设这个四面体的四个顶点分别为ABCD，依次利用对立事件的概率求解.

由题意知本题是一个等可能事件的概率，假设这个四面体的四个顶点分别为ABCD，

蚂蚁从A开始爬，如果爬到第三次时，蚂蚁在A点，那么第四次就一定不在A点，

设蚂蚁第三次在A点的概率为，则它爬了4米之后恰好位于顶点A的概率为，

设蚂蚁第二次在A点的概率为，则,

显然蚂蚁第一次爬完之后在A点的概率为0，则，可得，代入，

得它爬了4米之后恰好位于顶点A的概率为.

故选：