题目内容
若椭圆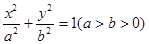 的离心率为
的离心率为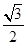 ,则双曲线
,则双曲线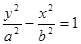 的渐近线方程为
的渐近线方程为
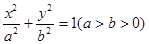 的离心率为
的离心率为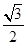 ,则双曲线
,则双曲线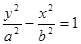 的渐近线方程为
的渐近线方程为A.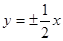 | B.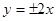 | C.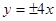 | D.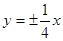 |
A
分析:根据题意,结合椭圆的性质,可得e2=
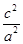 ="1-"
="1-" 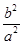 =
= 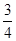 ,进而可得
,进而可得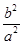 =
= 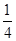 ;再由双曲线的渐进性方程,可得答案.
;再由双曲线的渐进性方程,可得答案.解:根据题意,椭圆
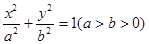 的离心率为
的离心率为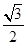 ,
,则有e2=
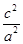 ="1-"
="1-" 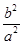 =
= 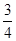 ,
,即
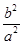 =
= 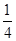 ;
;则双曲线
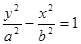 的渐近线方程为y=±
的渐近线方程为y=±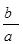 x,即y=±
x,即y=±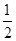 x;
x;故选A.

练习册系列答案
相关题目
题目内容
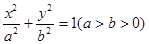 的离心率为
的离心率为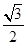 ,则双曲线
,则双曲线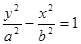 的渐近线方程为
的渐近线方程为A.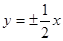 | B.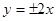 | C.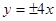 | D.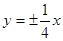 |
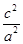 ="1-"
="1-" 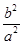 =
= 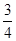 ,进而可得
,进而可得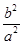 =
= 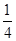 ;再由双曲线的渐进性方程,可得答案.
;再由双曲线的渐进性方程,可得答案.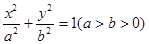 的离心率为
的离心率为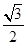 ,
,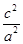 ="1-"
="1-" 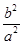 =
= 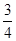 ,
,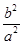 =
= 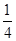 ;
;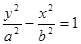 的渐近线方程为y=±
的渐近线方程为y=±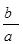 x,即y=±
x,即y=±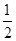 x;
x;