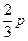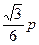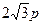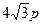题目内容
(本小题满分14分)
给定椭圆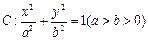 ,称圆心在坐标原点
,称圆心在坐标原点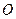 ,半径为
,半径为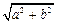 的圆是椭圆
的圆是椭圆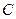 的“伴随圆”. 若椭圆C的一个焦点为
的“伴随圆”. 若椭圆C的一个焦点为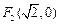 ,其短轴上的一个端点到
,其短轴上的一个端点到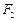 距离为
距离为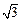 .
.
(Ⅰ)求椭圆C及其“伴随圆”的方程;
(Ⅱ)若过点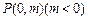 的直线
的直线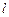 与椭圆C只有一个公共点,且
与椭圆C只有一个公共点,且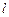 截椭圆C的“伴随圆”所得的弦长为
截椭圆C的“伴随圆”所得的弦长为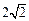 ,求
,求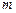 的值;
的值;
(Ⅲ)过椭圆C“伴椭圆”上一动点Q作直线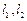 ,使得
,使得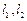 与椭圆C都只有一个公共点,试判断直线
与椭圆C都只有一个公共点,试判断直线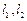 的斜率之积是否
的斜率之积是否 为定值,并说明理由.
为定值,并说明理由.
给定椭圆
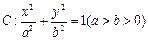 ,称圆心在坐标原点
,称圆心在坐标原点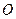 ,半径为
,半径为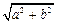 的圆是椭圆
的圆是椭圆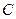 的“伴随圆”. 若椭圆C的一个焦点为
的“伴随圆”. 若椭圆C的一个焦点为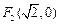 ,其短轴上的一个端点到
,其短轴上的一个端点到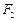 距离为
距离为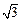 .
.(Ⅰ)求椭圆C及其“伴随圆”的方程;
(Ⅱ)若过点
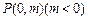 的直线
的直线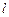 与椭圆C只有一个公共点,且
与椭圆C只有一个公共点,且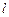 截椭圆C的“伴随圆”所得的弦长为
截椭圆C的“伴随圆”所得的弦长为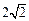 ,求
,求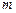 的值;
的值;(Ⅲ)过椭圆C“伴椭圆”上一动点Q作直线
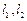 ,使得
,使得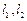 与椭圆C都只有一个公共点,试判断直线
与椭圆C都只有一个公共点,试判断直线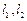 的斜率之积是否
的斜率之积是否 为定值,并说明理由.
为定值,并说明理由.解:(Ⅰ)由题意得: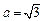 ,半焦距
,半焦距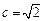
则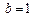 椭圆C方程为
椭圆C方程为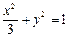
“伴随圆”方程为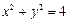 ……………3分
……………3分
(Ⅱ)则设过点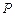 且与椭圆有一个交点的直线
且与椭圆有一个交点的直线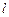 为:
为: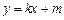 ,
,
则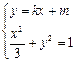 整理得
整理得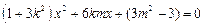
所以 ,解
,解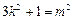
 ① ……………5分
① ……………5分
又因为直线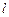 截椭圆
截椭圆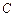 的“伴随圆”所得的弦长为
的“伴随圆”所得的弦长为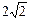 ,
,
则有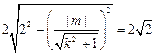 化简得
化简得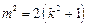 ② ……………7分
② ……………7分
联立①②解得,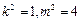 ,
,
所以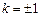 ,
,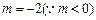 ,则
,则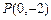 ……………8分
……………8分
(Ⅲ)当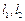 都有斜率时,设点
都有斜率时,设点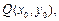 其中
其中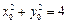 ,
,
设经过点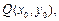 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为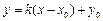 ,
,
由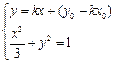 ,消去
,消去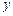 得到
得到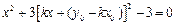 ……………10分
……………10分
即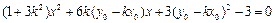 ,
,  ,
,
经过化简得到: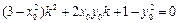 , ……………12分
, ……………12分
因为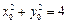 ,所以有
,所以有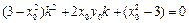 ,
,
设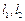 的斜率分别为
的斜率分别为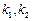
 ,因为
,因为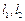 与椭圆都只有一个公共点,
与椭圆都只有一个公共点,
所以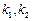 满足方程
满足方程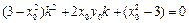 ,
,
因而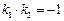 ,即直线
,即直线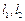 的斜率之积是为定值
的斜率之积是为定值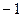
 ……………14分
……………14分
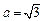 ,半焦距
,半焦距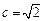
则
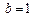 椭圆C方程为
椭圆C方程为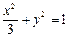
“伴随圆”方程为
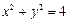 ……………3分
……………3分(Ⅱ)则设过点
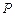 且与椭圆有一个交点的直线
且与椭圆有一个交点的直线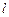 为:
为: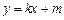 ,
, 则
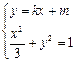 整理得
整理得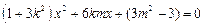
所以
 ,解
,解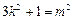
 ① ……………5分
① ……………5分又因为直线
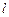 截椭圆
截椭圆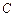 的“伴随圆”所得的弦长为
的“伴随圆”所得的弦长为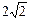 ,
,则有
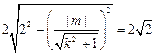 化简得
化简得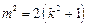 ② ……………7分
② ……………7分联立①②解得,
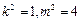 ,
,所以
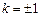 ,
,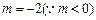 ,则
,则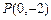 ……………8分
……………8分(Ⅲ)当
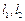 都有斜率时,设点
都有斜率时,设点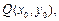 其中
其中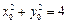 ,
,设经过点
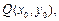 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为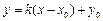 ,
,由
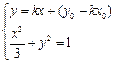 ,消去
,消去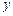 得到
得到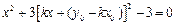 ……………10分
……………10分即
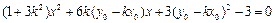 ,
,  ,
, 经过化简得到:
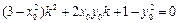 , ……………12分
, ……………12分因为
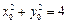 ,所以有
,所以有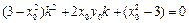 ,
,设
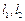 的斜率分别为
的斜率分别为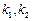
 ,因为
,因为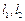 与椭圆都只有一个公共点,
与椭圆都只有一个公共点,所以
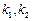 满足方程
满足方程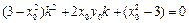 ,
,因而
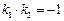 ,即直线
,即直线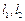 的斜率之积是为定值
的斜率之积是为定值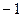
 ……………14分
……………14分略

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
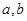 的等差中项是
的等差中项是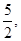 一个等比中项是
一个等比中项是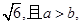 则双曲线
则双曲线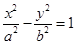 的离心率
的离心率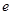 等于
等于 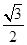
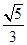
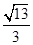
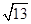
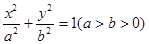 的离心率为
的离心率为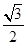 ,则双曲线
,则双曲线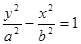 的渐近线方程为
的渐近线方程为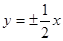
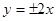
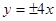
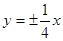
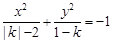 表示焦点在
表示焦点在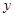 轴上的双曲线,那么它的半焦距
轴上的双曲线,那么它的半焦距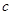 的取值范围是
的取值范围是 
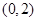
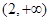
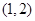
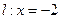 ,
,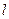 与
与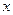 轴交于点
轴交于点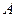 ,动点
,动点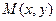 到直线
到直线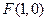 的距离大
的距离大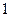 .
.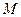 的轨迹
的轨迹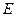
 的方程;
的方程; 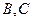 两点,若
两点,若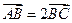 ,求此直线的方程.
,求此直线的方程.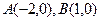 的距离之比等于2的点的轨迹方程。
的距离之比等于2的点的轨迹方程。 ABC的顶点A(-5,0), B(5,0),顶点C在双曲线
ABC的顶点A(-5,0), B(5,0),顶点C在双曲线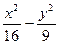 =1上,则
=1上,则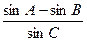 的值为 。
的值为 。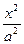 -
-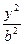 =1(a>0,b>0)的焦点,而且被该双曲线的右准线分成的弧长为2∶1的两段圆弧,那么该双曲线的离心率e等于
=1(a>0,b>0)的焦点,而且被该双曲线的右准线分成的弧长为2∶1的两段圆弧,那么该双曲线的离心率e等于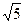
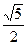

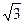
 上,则这个正三角形的边长为
上,则这个正三角形的边长为