题目内容
椭圆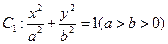 的长轴长为4,焦距为2,F1、F2分别为椭圆的左、右焦点,直线
的长轴长为4,焦距为2,F1、F2分别为椭圆的左、右焦点,直线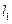 过点
过点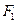 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线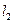 垂直
垂直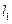 于点
于点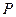 ,线段
,线段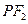 垂直平分线交
垂直平分线交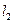 于点
于点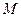
(1)求椭圆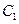 的标准方程和动点
的标准方程和动点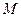 的轨迹
的轨迹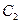 的方程。
的方程。
(2)过椭圆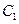 的右焦点
的右焦点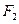 作斜率为1的直线交椭圆于A、B两点,求
作斜率为1的直线交椭圆于A、B两点,求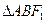 的面积。
的面积。
(3)设轨迹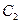 与
与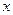 轴交于点
轴交于点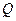 ,不同的两点
,不同的两点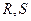 在轨迹
在轨迹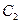 上,
上,
满足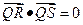 求证:直线
求证:直线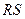 恒过
恒过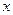 轴上的定点。
轴上的定点。
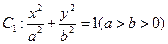 的长轴长为4,焦距为2,F1、F2分别为椭圆的左、右焦点,直线
的长轴长为4,焦距为2,F1、F2分别为椭圆的左、右焦点,直线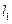 过点
过点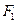 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线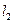 垂直
垂直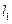 于点
于点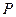 ,线段
,线段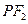 垂直平分线交
垂直平分线交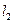 于点
于点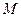
(1)求椭圆
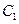 的标准方程和动点
的标准方程和动点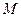 的轨迹
的轨迹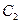 的方程。
的方程。(2)过椭圆
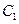 的右焦点
的右焦点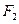 作斜率为1的直线交椭圆于A、B两点,求
作斜率为1的直线交椭圆于A、B两点,求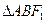 的面积。
的面积。(3)设轨迹
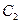 与
与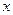 轴交于点
轴交于点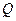 ,不同的两点
,不同的两点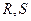 在轨迹
在轨迹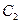 上,
上,满足
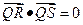 求证:直线
求证:直线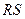 恒过
恒过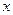 轴上的定点。
轴上的定点。解:(1)由题设知:2a = 4,即a = 2,2c=2,即c=1,
故椭圆方程为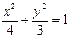 , ………2分
, ………2分
∵MP=MF2,
∴动点M到定直线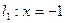 的距离等于它到定点F1(1,0)的距离,
的距离等于它到定点F1(1,0)的距离,
∴动点M的轨迹是C为l1准线,F2为焦点的抛物线
∴点M的轨迹C2的方程为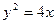 …………5分
…………5分
(2)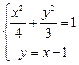 消去
消去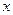 并整理得:
并整理得: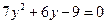
设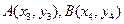 则
则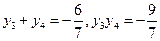 ---------------7分
---------------7分
 =
=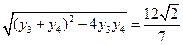 -----------9分
-----------9分
(3)Q(0,0),设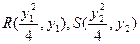
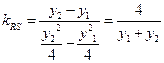 ------------10分
------------10分
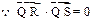
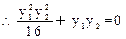
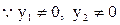
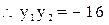
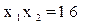 ---------------------------11分
---------------------------11分
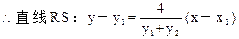
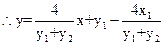
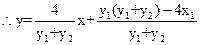
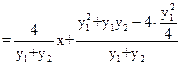
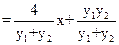
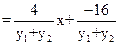
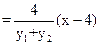 ----------------13 分
----------------13 分
故直线RS恒过定点(4,0)-------------------------------------------------------14分

故椭圆方程为
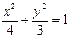 , ………2分
, ………2分∵MP=MF2,
∴动点M到定直线
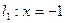 的距离等于它到定点F1(1,0)的距离,
的距离等于它到定点F1(1,0)的距离,∴动点M的轨迹是C为l1准线,F2为焦点的抛物线
∴点M的轨迹C2的方程为
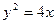 …………5分
…………5分(2)
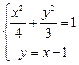 消去
消去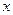 并整理得:
并整理得: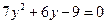
设
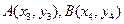 则
则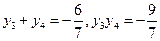 ---------------7分
---------------7分 =
=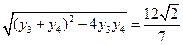 -----------9分
-----------9分(3)Q(0,0),设
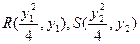
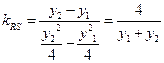 ------------10分
------------10分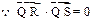
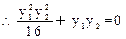
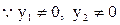
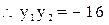
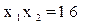 ---------------------------11分
---------------------------11分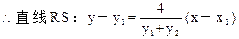
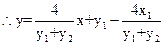
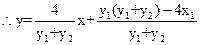
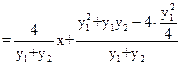
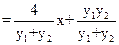
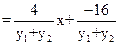
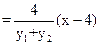 ----------------13 分
----------------13 分 故直线RS恒过定点(4,0)-------------------------------------------------------14分
略

练习册系列答案
相关题目
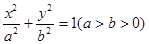 的离心率为
的离心率为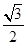 ,则双曲线
,则双曲线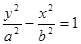 的渐近线方程为
的渐近线方程为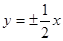
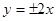
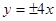
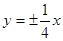
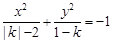 表示焦点在
表示焦点在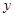 轴上的双曲线,那么它的半焦距
轴上的双曲线,那么它的半焦距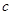 的取值范围是
的取值范围是 
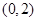
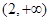
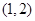
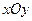 中,设点
中,设点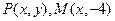 ,以线段
,以线段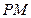 为直径的圆经过原点
为直径的圆经过原点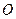 .
.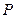 的轨迹
的轨迹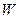 的方程;
的方程;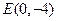 的直线
的直线 与轨迹
与轨迹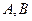 ,点
,点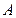 关于
关于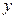 轴的对称点为
轴的对称点为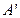 ,试判断直线
,试判断直线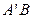 是否恒过一定点,并证明你的结论.
是否恒过一定点,并证明你的结论.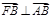 时,其离心率为
时,其离心率为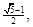 此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于( )
此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于( ) 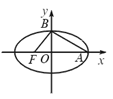
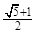
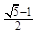
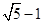
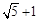
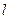 :
: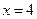 ,定点
,定点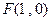 ,动点
,动点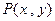 到直线
到直线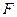 的距离的2倍.
的距离的2倍. 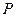 的轨迹
的轨迹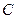 的方程;
的方程;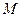 为轨迹
为轨迹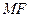 长为半径作圆
长为半径作圆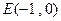 可作圆
可作圆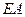 ,
,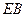 (
(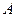 ,
,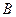 为切点),求四边形
为切点),求四边形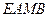 面积的最大值.
面积的最大值.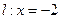 ,
,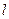 与
与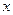 轴交于点
轴交于点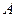 ,动点
,动点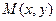 到直线
到直线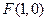 的距离大
的距离大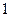 .
.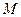 的轨迹
的轨迹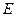
 的方程;
的方程; 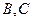 两点,若
两点,若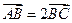 ,求此直线的方程.
,求此直线的方程.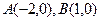 的距离之比等于2的点的轨迹方程。
的距离之比等于2的点的轨迹方程。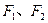 为椭圆
为椭圆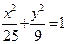 的两个焦点,过
的两个焦点,过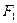 的直线交椭圆于A、B两点,若
的直线交椭圆于A、B两点,若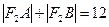 ,则
,则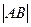 =_______.
=_______.