题目内容
已知椭圆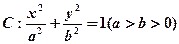 的焦距为2,点
的焦距为2,点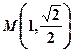 在椭圆
在椭圆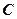 上,
上,
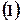 求椭圆
求椭圆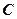 的标准方程;
的标准方程;
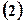 若过点
若过点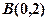 的直线与
的直线与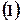 中的椭圆交于不同的两点
中的椭圆交于不同的两点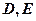 (
(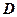 在
在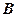 、
、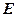 之间);
之间);
试求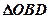 与
与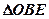 面积之比的取值范围.
面积之比的取值范围.
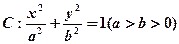 的焦距为2,点
的焦距为2,点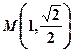 在椭圆
在椭圆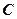 上,
上,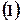 求椭圆
求椭圆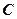 的标准方程;
的标准方程;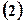 若过点
若过点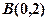 的直线与
的直线与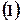 中的椭圆交于不同的两点
中的椭圆交于不同的两点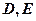 (
(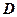 在
在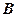 、
、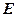 之间);
之间);试求
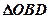 与
与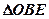 面积之比的取值范围.
面积之比的取值范围.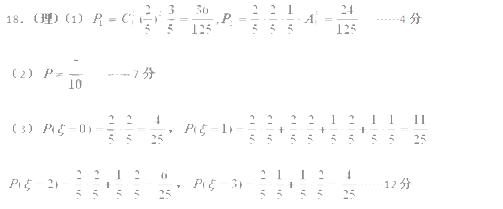
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
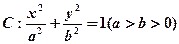 的焦距为2,点
的焦距为2,点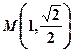 在椭圆
在椭圆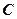 上,
上,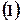 求椭圆
求椭圆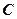 的标准方程;
的标准方程;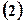 若过点
若过点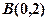 的直线与
的直线与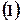 中的椭圆交于不同的两点
中的椭圆交于不同的两点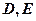 (
(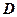 在
在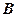 、
、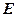 之间);
之间);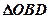 与
与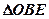 面积之比的取值范围.
面积之比的取值范围.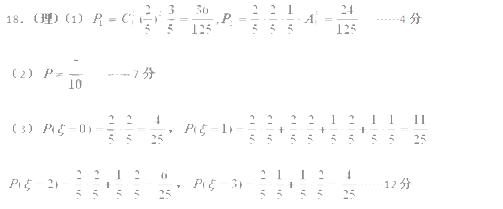

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案