Question

【题目】已知抛物线C:x24py（p为大于2的质数）的焦点为F，过点F且斜率为k(k0)的直线交C于A，B两点，线段AB的垂直平分线交y轴于点E，抛物线C在点A，B处的切线相交于点G.记四边形AEBG的面积为S.

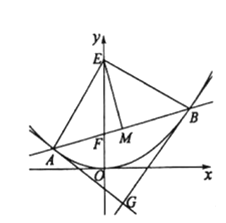
（1）求点G的轨迹方程；

（2）当点G的横坐标为整数时，S是否为整数？若是，请求出所有满足条件的S的值；若不是，请说明理由.

Answer 1

【答案】（1）（2）当G点横坐标为整数时，S不是整数．

【解析】

（1）先求解导数，得出切线方程，联立方程得出交点G的轨迹方程；

（2）先求解弦长，再分别求解点到直线的距离，表示出四边形的面积，结合点G的横坐标为整数进行判断.

（1）设，则，

抛物线C的方程可化为，则，

所以曲线C在点A处的切线方程为，

在点B处的切线方程为，

因为两切线均过点G，所以，

所以A，B两点均在直线上，所以直线AB的方程为，

又因为直线AB过点F(0，p)，所以，即G点轨迹方程为；

（2）设点G(，)，由（1）可知，直线AB的方程为，

即，

将直线AB的方程与抛物线联立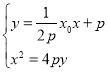，，整理得，

所以，，解得，

因为直线AB的斜率，所以，

且，

线段AB的中点为M，

所以直线EM的方程为：，

所以E点坐标为(0，)，

直线AB的方程整理得，

则G到AB的距离，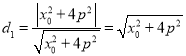

则E到AB的距离，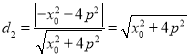

所以，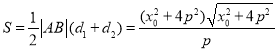

设，因为p是质数，且为整数，所以或，

当时，，是无理数，不符题意，

当时，，

因为当时，，即是无理数，所以不符题意，

当时，是无理数，不符题意，

综上，当G点横坐标为整数时，S不是整数．