题目内容
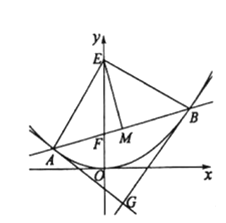
【题目】某地为改善旅游环境进行景点改造.如图,将两条平行观光道l1和l2通过一段抛物线形状的栈道AB连通(道路不计宽度),l1和l2所在直线的距离为0.5(百米),对岸堤岸线l3平行于观光道且与l2相距1.5(百米)(其中A为抛物线的顶点,抛物线的对称轴垂直于l3,且交l3于M),在堤岸线l3上的E,F两处建造建筑物,其中E,F到M的距离为1(百米),且F恰在B的正对岸(即BF⊥l3).
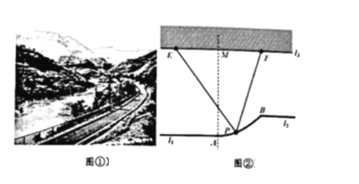
(1)在图②中建立适当的平面直角坐标系,并求栈道AB的方程;
(2)游客(视为点P)在栈道AB的何处时,观测EF的视角(∠EPF)最大?请在(1)的坐标系中,写出观测点P的坐标.
【答案】(1)见解析,![]() ,x
,x![]() [0,1];(2)P(
[0,1];(2)P(![]() ,
,![]() )时,视角∠EPF最大.
)时,视角∠EPF最大.
【解析】
(1)以A为原点,l1为x轴,抛物线的对称轴为y轴建系,设出方程,通过点![]() 的坐标可求方程;
的坐标可求方程;
(2)设出![]() 的坐标,表示出
的坐标,表示出![]() ,利用基本不等式求解
,利用基本不等式求解![]() 的最大值,从而可得观测点P的坐标.
的最大值,从而可得观测点P的坐标.
(1)以A为原点,l1为x轴,抛物线的对称轴为y轴建系
由题意知:B(1,0.5),设抛物线方程为![]()
代入点B得:p=1,故方程为![]() ,x
,x![]() [0,1];
[0,1];
(2)设P(![]() ,
,![]() ),t
),t![]() [0,
[0,![]() ],作PQ⊥l3于Q,记∠EPQ=
],作PQ⊥l3于Q,记∠EPQ=![]() ,∠FPQ=
,∠FPQ=![]()
![]() ,
,![]() ,
,![]()
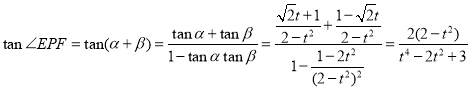
令![]() ,
,![]() ,则:
,则:
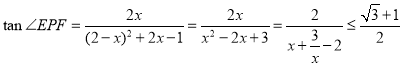 ,
,
当且仅当![]() 即
即![]() ,即
,即![]() ,即
,即![]() 时取等号;
时取等号;
故P(![]() ,
,![]() )时视角∠EPF最大,
)时视角∠EPF最大,
答:P(![]() ,
,![]() )时,视角∠EPF最大.
)时,视角∠EPF最大.

练习册系列答案
相关题目
【题目】已知函数![]() ,
,![]()
![]() .
.
(1)当x≥0时,f(x)≤h(x)恒成立,求a的取值范围;
(2)当x<0时,研究函数F(x)=h(x)﹣g(x)的零点个数;
(3)求证:![]() (参考数据:ln1.1≈0.0953).
(参考数据:ln1.1≈0.0953).