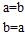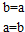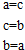题目内容
18.已知复数z1满足(z1-2)(1+i)=1-i(i为虚数单位),求z1的模及共轭复数.分析 设 Z1=a+bi,通过复数相等求出z1=2-i,然后求出模以及复数的共轭复数.
解答 解:(Z1-2)( 1+i)=1-i,
设 Z1=a+bi,
则 (a+bi-2)( 1+i)=1-i,
展开整理得:(a-b-2)+(a+b-2)i=1-i,
比较得:$\left\{\begin{array}{l}a-b-2=1\\ a+b-2=-1\end{array}\right.$,
解得:b=-1,a=2所以z1=2-i,
|Z1|=|2-i|=$\sqrt{5}$ $\overline{z}$=2+i.
点评 本题考查复数的基本运算,基本知识的考查.

练习册系列答案
相关题目
8.(1-x-3y)5的展开式中不含x的项的系数和为( )
| A. | 32 | B. | -32 | C. | 64 | D. | -64 |
3.已知z1,z2是复数,下列结论错误的是( )
| A. | 若|z1-z2|=0,则$\overline{{z}_{1}}$=$\overline{{z}_{2}}$ | B. | 若 z1=$\overline{{z}_{2}}$,则$\overline{{z}_{1}}$=z2 | ||
| C. | 若|z1|=|z2|,则z1•$\overline{{z}_{1}}$=z2$\overline{{z}_{2}}$ | D. | 若|z1|=|z2|,则z12=z22 |
7.已知A={x|1≤x≤5},B={x|(x-a+1)(x-a-1)≤0},条件p:x∈A,条件q:x∈B,若?p是?q的充分不必要条件,则实数a的取值范围是( )
| A. | (2,4] | B. | [2,4] | C. | [2,4) | D. | (2,4) |