题目内容
18.若数列{xn}满足:$\frac{1}{{{x_{n+1}}}}-\frac{1}{x_n}$=d(d为常数,n∈N*),则称{xn}为调和数列.已知数列{an}为调和数列,且a1=1,$\frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}+\frac{1}{a_4}+\frac{1}{a_5}$=15.(Ⅰ)求数列{an}的通项an;
(Ⅱ)数列$\left\{{\frac{2^n}{a_n}}\right\}$的前n项和为Sn,是否存在正整数n,使得Sn≥2015?若存在,求出n的取值集合;若不存在,请说明理由.
分析 (Ⅰ)通过$\left\{{\frac{1}{a_n}}\right\}$为等差数列,及$\frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}+\frac{1}{a_4}+\frac{1}{a_5}$=15,利用等差中项的性质计算即得结论;
(Ⅱ)通过写出Sn、2Sn的表达式,;利用错位相减法可得Sn,结合Sn递增,计算即可.
解答 解:(Ⅰ)依题意$\left\{{\frac{1}{a_n}}\right\}$为等差数列,
由$\frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}+\frac{1}{a_4}+\frac{1}{a_5}$=15,
得:$\frac{5}{a_3}=15$,即$\frac{1}{a_3}=3$,
∴公差$d=\frac{{\frac{1}{a_3}-\frac{1}{a_1}}}{2}=1$,故$\frac{1}{a_n}=n$,
即${a_n}=\frac{1}{n}$;
(Ⅱ)${S_n}=1×{2^1}+2×{2^2}+…+n×{2^n}$ ①
2Sn=1×22+…+(n-1)2n+n×2n+1 ②
②-①得:${S_n}=n×{2^{n+1}}-({2+{2^2}+…+{2^n}})$=(n-1)2n+1+2,
由于Sn是递增的,当n=7时,${S_7}=6×{2^8}+2<2015$;
当n=8时,${S_8}=7×{2^9}+2>{2^{11}}>2015$.
所以存在正整数m,使得Sn≥2015,
∴n的取值集合为{n|n≥8,n∈N*}.
点评 本题考查求数列的通项、前n项和,注意解题方法的积累,属于中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
13.如图,三个边长为2的等边三角形有一条边在同一条直线上,边B3C3上有10个不同的点P1,P2,…P10,记mi=$\overrightarrow{A{B_2}}•\overrightarrow{A{P_i}}$(i=1,2,…,10),则m1+m2+…+m10的值为( )

| A. | 180 | B. | $60\sqrt{3}$ | C. | 45 | D. | $15\sqrt{3}$ |
3.某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的相关数据,如表所示.
已知这100位顾客中的一次购物量超过8件的顾客占55%.
(1)求x,y的值.
(2)求顾客一次购物的结算时间超过2分钟的概率.
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件以上 |
| 顾客数(人) | x | 30 | 25 | y | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
(1)求x,y的值.
(2)求顾客一次购物的结算时间超过2分钟的概率.
10.若cosθ=-$\frac{{\sqrt{5}}}{5}$,θ∈[0,π],则tanθ=( )
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
7.某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费xi和年销售量yi(i=1,2,3,..8)数据作了初步处理,得到下面的散点图及一些统计量的值.
表中:${w_i}=\sqrt{x_i}$ $\overline{w}$=$\sum_{i=1}^{8}$wi
(Ⅰ)根据散点图判断,y=a+bx与$y=c+d\sqrt{x}$,哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);
(Ⅱ)根据(I)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x,y的关系为z=0.2y-x,根据(II)的结果回答下列问题:
(i)当年宣传费x=49时,年销售量及年利润的预报值时多少?
(ii)当年宣传费x为何值时,年利润的预报值最大?并求出最大值
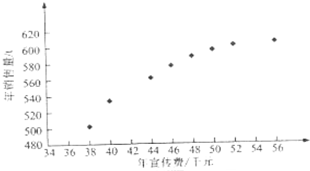
| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{8}$(xi-$\overline{x}$)2 | $\sum_{i=1}^{8}$(wi-$\overline{w}$)2 | $\sum_{i=1}^{8}$(xi-$\overline{x}$)(yi-$\overline{y}$) | $\sum_{i=1}^{8}$(wi-$\overline{w}$)(yi-$\overline{y}$) |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
(Ⅰ)根据散点图判断,y=a+bx与$y=c+d\sqrt{x}$,哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);
(Ⅱ)根据(I)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x,y的关系为z=0.2y-x,根据(II)的结果回答下列问题:
(i)当年宣传费x=49时,年销售量及年利润的预报值时多少?
(ii)当年宣传费x为何值时,年利润的预报值最大?并求出最大值

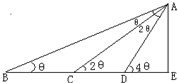 如图在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进15m,至点C处测得顶端A的仰角为2θ,再继续前进5$\sqrt{3}$m至D点,测得顶端A的仰角为4θ,则建筑物AE的高为$\frac{15}{2}$m.
如图在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进15m,至点C处测得顶端A的仰角为2θ,再继续前进5$\sqrt{3}$m至D点,测得顶端A的仰角为4θ,则建筑物AE的高为$\frac{15}{2}$m.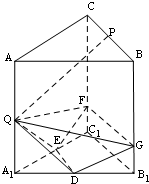 如图所示,正三棱柱ABC-A1B1C1中,P,Q,D,E分别是所在棱的中点,F,G是分别BB1,CC1上的点,满足$\frac{BG}{{G{B_1}}}=\frac{CF}{{F{C_1}}}$=3.
如图所示,正三棱柱ABC-A1B1C1中,P,Q,D,E分别是所在棱的中点,F,G是分别BB1,CC1上的点,满足$\frac{BG}{{G{B_1}}}=\frac{CF}{{F{C_1}}}$=3.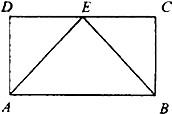 如图,在矩形ABCD中,点E为边CD上任意一点,现有质地均匀的粒子散落在矩形ABCD内,则粒子落在△ABE内的概率等于$\frac{1}{2}$.
如图,在矩形ABCD中,点E为边CD上任意一点,现有质地均匀的粒子散落在矩形ABCD内,则粒子落在△ABE内的概率等于$\frac{1}{2}$.