题目内容
13．如图，三个边长为2的等边三角形有一条边在同一条直线上，边B3C3上有10个不同的点P1，P2，…P10，记mi=$\overrightarrow{A{B_2}}•\overrightarrow{A{P_i}}$（i=1，2，…，10），则m1+m2+…+m10的值为（ ）
| A． | 180 | B． | $60\sqrt{3}$ | C． | 45 | D． | $15\sqrt{3}$ |
分析 由题意可得$\overrightarrow{A{B}_{2}}⊥\overrightarrow{{B}_{3}{C}_{3}}$，然后把mi=$\overrightarrow{A{B_2}}•\overrightarrow{A{P_i}}$转化为$\overrightarrow{A{B}_{2}}•\overrightarrow{A{C}_{3}}$求得答案．
解答 解：由图可知，∠B2AC3=30°，又∠AC3B3=60°，
∴$\overrightarrow{A{B}_{2}}⊥\overrightarrow{{B}_{3}{C}_{3}}$，即$\overrightarrow{A{B}_{2}}•\overrightarrow{{B}_{3}{C}_{3}}=0$．
则${m_i}=\overrightarrow{A{B_2}}•\overrightarrow{A{P_i}}=\overrightarrow{A{B_2}}（\overrightarrow{A{C_3}}+\overrightarrow{{C_3}{P_i}}）=\overrightarrow{A{B_2}}•\overrightarrow{A{C_3}}=2\sqrt{3}×6×\frac{{\sqrt{3}}}{2}=18$，
∴m1+m2+…+m10=18×10=180．
故选：A．
点评 本题考查平面向量的数量积运算，考查了三角形中边角关系的运用，考查了数学转化思想方法，是中档题．
练习册系列答案
相关题目
已知A、B分别为曲线C：$\frac{{x}^{2}}{{a}^{2}}$+y2=1（a＞0）与x轴的左、右两个交点，直线l过点B且与x轴垂直，P为l上异于点B的点，连结AP与曲线C交于点M．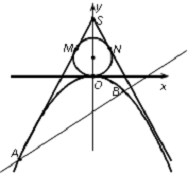
如图所示，已知点S（0，3），过点S作直线SM，SN与圆Q：x2+y2-2y=0和抛物线C：x2=-2py（p＞0）都相切．