题目内容
6. 如图,在矩形ABCD中,点E为边CD上任意一点,现有质地均匀的粒子散落在矩形ABCD内,则粒子落在△ABE内的概率等于$\frac{1}{2}$.
如图,在矩形ABCD中,点E为边CD上任意一点,现有质地均匀的粒子散落在矩形ABCD内,则粒子落在△ABE内的概率等于$\frac{1}{2}$.
分析 由题意,只要求出矩形和三角形的面积,利用面积比得到所求.
解答 解:由题意,本题符合几何概型,假设矩形ABCD的面积为S,则△ABE的面积为$\frac{1}{2}$S,
由几何概型公式可得粒子落在△ABE内的概率等于:$\frac{1}{2}$;
故答案为:$\frac{1}{2}$.
点评 本题考查了几何概型概率求法;根据是明确满足条件的事件的测度是什么,利用公式解答.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
16.若框图所给的程序运行结果为S=90.那么判断框中应填入后的条件是( )
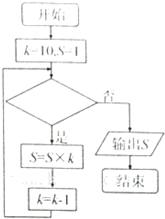

| A. | k=9 | B. | k≤8 | C. | k<8 | D. | k>8 |
14.甲、乙两位同学各拿出六张游戏牌,用作投骰子的奖品,两人商定:骰子朝上的面的点数为奇数时甲得1分,否则乙得1分,先积得3分者获胜得所有12张游戏牌,并结束游戏.比赛开始后,甲积2分,乙积1分,这时因意外事件中断游戏,以后他们不想再继续这场游戏,下面对这12张游戏牌的分配合理的是( )
| A. | 甲得9张,乙得3张 | B. | 甲得6张,乙得6张 | ||
| C. | 甲得8张,乙得4张 | D. | 甲得10张,乙得2张 |
11.把函数f(x)=sinx(x∈[0,2π])的图象向右平移$\frac{π}{3}$个单位后得到函数g(x)的图象,则f(x)与g(x)的图象所围成的面积为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | 2 |
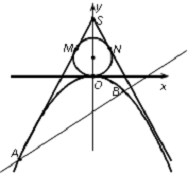 如图所示,已知点S(0,3),过点S作直线SM,SN与圆Q:x2+y2-2y=0和抛物线C:x2=-2py(p>0)都相切.
如图所示,已知点S(0,3),过点S作直线SM,SN与圆Q:x2+y2-2y=0和抛物线C:x2=-2py(p>0)都相切.