题目内容
10.若cosθ=-$\frac{{\sqrt{5}}}{5}$,θ∈[0,π],则tanθ=( )| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
分析 由cosθ的值及θ的范围,利用同角三角函数间的基本关系求出sinθ的值,即可确定出tanθ的值.
解答 解:∵cosθ=-$\frac{{\sqrt{5}}}{5}$<0,θ∈[0,π],
∴θ∈($\frac{π}{2}$,π],
∴sinθ=$\sqrt{1-co{s}^{2}θ}$=$\frac{2\sqrt{5}}{5}$,
则tanθ=$\frac{sinθ}{cosθ}$=-2,
故选:A.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
19.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:cm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如表:
甲厂:
乙厂:
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面2×2列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
附K2=$\frac{n(ad-bc)2}{(a+b)(c+d)(a+c)(b+d)}$,
甲厂:
| 分组 | [29.86, 29.90 ) | [29.90, 29.94) | [29.94, 29.98) | [29.9 8, 30.02) | [30.02, 30.06) | [30.06, 30.10) | [30.10, 30.14) |
| 频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
| 分组 | [29.86, 29.90) | [29.90, 29.94) | [29.94, 29.98) | [29.98, 30.02) | [30.02, 30.06) | [30.06, 30.10) | [30.10, 30.14) |
| 频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
(2)由以上统计数据填下面2×2列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
| 甲厂 | 乙厂 | 合计 | |
| 优质品 | |||
| 非优质品 | |||
| 合计 |
| p(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
20.命题“?x∈R,sin2x>1”的否定是( )
| A. | ?x∈R,sin2x≤1 | B. | ?x∉R,sin2x>1 | C. | ?x0∈R,sin2x≤1 | D. | ?x0∉R,sin2x>1 |
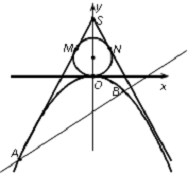 如图所示,已知点S(0,3),过点S作直线SM,SN与圆Q:x2+y2-2y=0和抛物线C:x2=-2py(p>0)都相切.
如图所示,已知点S(0,3),过点S作直线SM,SN与圆Q:x2+y2-2y=0和抛物线C:x2=-2py(p>0)都相切.