题目内容
9.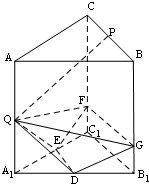 如图所示,正三棱柱ABC-A1B1C1中,P,Q,D,E分别是所在棱的中点,F,G是分别BB1,CC1上的点,满足$\frac{BG}{{G{B_1}}}=\frac{CF}{{F{C_1}}}$=3.
如图所示,正三棱柱ABC-A1B1C1中,P,Q,D,E分别是所在棱的中点,F,G是分别BB1,CC1上的点,满足$\frac{BG}{{G{B_1}}}=\frac{CF}{{F{C_1}}}$=3.(Ⅰ)证明:PQ∥平面DEFG;
(Ⅱ)若该三棱柱的所有棱长为2,求四棱锥Q-DEFG的体积.
分析 (Ⅰ)连接BQ,CQ,解直角三角形可得BQ∥GD,CQ∥FE,然后利用面面平行的判定证明平面QBC∥平面DEFG;
(Ⅱ)延长GD,FE,QA1,则三线必相交于一点O,把四棱锥Q-DEFG的体积转化为三棱锥G-OQF的体积得答案.
解答 (Ⅰ)证明:如图,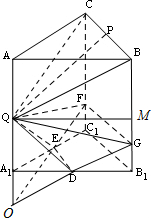 连接BQ,CQ,
连接BQ,CQ,
取BB1中点M,连接QM,则△BMQ为Rt△,
在Rt△BMQ中,tan∠QBM=$\frac{QM}{BM}$,
在Rt△GB1D中,tan∠GB1D=$\frac{D{B}_{1}}{G{B}_{1}}$=$\frac{\frac{1}{2}{A}_{1}{B}_{1}}{\frac{1}{2}M{B}_{1}}=\frac{QM}{BM}$,
∴∠∠QBM=∠GB1D,则BQ∥GD,
同理可证CQ∥FE,又BQ∩CQ=Q,则平面QBC∥平面DEFG;
(Ⅱ)延长GD,FE,QA1,则三线必相交于一点,设为O,
∵D、E分别是所在棱的中点,
故而DE∥FG,DE=$\frac{1}{2}FG$,∴${S}_{DEFG}=\frac{3}{4}{S}_{△OFG}$,
又∵三棱柱的所有棱长为2,∴OQ=$\frac{3}{2}$,
G到平面OQF的距离等于B到平面ACC1A1的距离,
而三角形ABC的边AC上的高线$\sqrt{3}$即为距离,也就是所求棱锥的高的值,
∴${V}_{Q-DEFG}=\frac{3}{4}{V}_{Q-OFG}=\frac{3}{4}{V}_{G-OQF}$=$\frac{3}{4}×\frac{1}{3}×\frac{1}{2}×\frac{3}{2}×2\sqrt{3}=\frac{3\sqrt{3}}{8}$.
点评 本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.

| A. | 甲得9张,乙得3张 | B. | 甲得6张,乙得6张 | ||
| C. | 甲得8张,乙得4张 | D. | 甲得10张,乙得2张 |
甲厂:
| 分组 | [29.86, 29.90 ) | [29.90, 29.94) | [29.94, 29.98) | [29.9 8, 30.02) | [30.02, 30.06) | [30.06, 30.10) | [30.10, 30.14) |
| 频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
| 分组 | [29.86, 29.90) | [29.90, 29.94) | [29.94, 29.98) | [29.98, 30.02) | [30.02, 30.06) | [30.06, 30.10) | [30.10, 30.14) |
| 频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
(2)由以上统计数据填下面2×2列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
| 甲厂 | 乙厂 | 合计 | |
| 优质品 | |||
| 非优质品 | |||
| 合计 |
| p(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
 如图是三棱柱被平面截去一部分后剩余的几何体的三视图,则截掉的几何体与三视图所示的几何体的体积之比为1:2.
如图是三棱柱被平面截去一部分后剩余的几何体的三视图,则截掉的几何体与三视图所示的几何体的体积之比为1:2.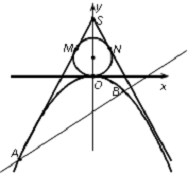 如图所示,已知点S(0,3),过点S作直线SM,SN与圆Q:x2+y2-2y=0和抛物线C:x2=-2py(p>0)都相切.
如图所示,已知点S(0,3),过点S作直线SM,SN与圆Q:x2+y2-2y=0和抛物线C:x2=-2py(p>0)都相切.