题目内容
8.设x,y满足约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y≥0}\\{2x+y≤1}\end{array}\right.$,记z=4x+y的最大值为a,则${∫}_{0}^{\frac{π}{a}}$(cos$\frac{x}{2}$-sin$\frac{x}{2}$)2dx=$\frac{π}{3}-\frac{1}{2}$.分析 作出不等式组对应的平面区域,利用目标函数的几何意义,即可求a,然后求解定积分.
解答 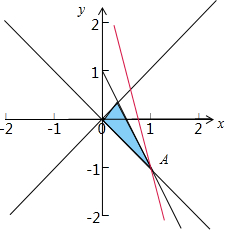 解:设z=4x+y,则只需求直线z=4x+y在y轴上的截距的最大值.
解:设z=4x+y,则只需求直线z=4x+y在y轴上的截距的最大值.
x,y满足约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y≥0}\\{2x+y≤1}\end{array}\right.$的可行域如图:
当直线与经过A时,截距最大,由$\left\{\begin{array}{l}x+y=0\\ 2x+y=1\end{array}\right.$,可得A(1,-1),解得a=3,
${∫}_{0}^{\frac{π}{a}}$(cos$\frac{x}{2}$-sin$\frac{x}{2}$)2dx=${∫}_{0}^{\frac{π}{3}}$(1-sinx)dx=(x+cosx)${|}_{0}^{\frac{π}{3}}$
=$\frac{π}{3}-\frac{1}{2}$.
故答案为:$\frac{π}{3}-\frac{1}{2}$.
点评 本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
相关题目
19.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:cm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如表:
甲厂:
乙厂:
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面2×2列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
附K2=$\frac{n(ad-bc)2}{(a+b)(c+d)(a+c)(b+d)}$,
甲厂:
| 分组 | [29.86, 29.90 ) | [29.90, 29.94) | [29.94, 29.98) | [29.9 8, 30.02) | [30.02, 30.06) | [30.06, 30.10) | [30.10, 30.14) |
| 频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
| 分组 | [29.86, 29.90) | [29.90, 29.94) | [29.94, 29.98) | [29.98, 30.02) | [30.02, 30.06) | [30.06, 30.10) | [30.10, 30.14) |
| 频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
(2)由以上统计数据填下面2×2列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
| 甲厂 | 乙厂 | 合计 | |
| 优质品 | |||
| 非优质品 | |||
| 合计 |
| p(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
20.命题“?x∈R,sin2x>1”的否定是( )
| A. | ?x∈R,sin2x≤1 | B. | ?x∉R,sin2x>1 | C. | ?x0∈R,sin2x≤1 | D. | ?x0∉R,sin2x>1 |