题目内容
【题目】在边长为4的正方形
的边上有一点
沿着折线
由点
(起点）向点
(终点）运动。设点运动的路程为
，
的面积为
，且与之间的函数关系式用如图所示的程序框图给出.
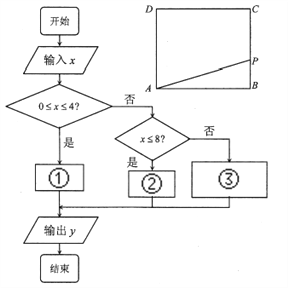
（1）写出框图中①、②、③处应填充的式子；
（2）若输出的面积值为6，则路程的值为多少？并指出此时点在正方形的什么位置上？
【答案】（1）
；（2）当
时，点
在正方形的
上；当
时，点在正方形的
上.
【解析】试题分析：（1）先求出定义域，然后根据点P的位置进行分类讨论，根据三角形的面积公式求出每一段△ABP的面积与P移动的路程间的函数关系式，最后用分段函数进行表示即可写出框图中①、②、③处应填充的式子；（2）利用△APB的面积为6，结合函数解析式，建立等式，即可求x的取值，进而得出此时点P的在正方形的什么位置上
试题解析：（1）由于x=0与x=12时，三点A、B、P不能构成三角形，故这个函数的
定义域为（0，12）．
当0＜x≤4时，S=f（x）=
4x=2x；
当4＜x≤8时，S=f（x）=8；
当8＜x＜12时，S=f（x）=4（12﹣x）=2（12﹣x）=24﹣2x．
∴这个函数的解析式为f（x）=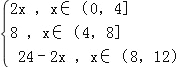
，
∴框图中①、②、③处应填充的式子分别为：y=2x，y=8，y=24﹣2x．
（2）若输出的面积y值为6，则
当0＜x≤4时，2x=6，∴x=3；
当8＜x＜12时，S=24﹣2x=6，∴x=9，
综上，当x=3时，此时点P的在正方形的边BC上，当x=9时，此时点P的在正方形的边DA上．
阅读快车系列答案
【题目】某地随着经济的发展，居民收入逐年增长，下表是该地一建设银行连续五年的储蓄存款（年底余额），如下表1：
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y（千亿元） | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便，工作人员将上表的数据进行了处理， 
得到下表2：
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
（Ⅰ）求z关于t的线性回归方程；
（Ⅱ）通过（Ⅰ）中的方程，求出y关于x的回归方程；
（Ⅲ）用所求回归方程预测到2020年年底，该地储蓄存款额可达多少？
（附：对于线性回归方程
，其中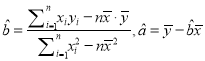
）
