题目内容
【题目】已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,且以线段
,且以线段![]() 为直径的圆与直线
为直径的圆与直线![]() 相切,椭圆
相切,椭圆![]() 截直线
截直线![]() 所得线段的长度为1.
所得线段的长度为1.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率的取值范围.
的斜率的取值范围.
【答案】(1)![]() ;(2)
;(2) .
.
【解析】
(1)根据直线与圆相切,以及椭圆中截得的弦长即可列方程求得![]() ,则问题得解;
,则问题得解;
(2)设出直线方程,联立椭圆方程,根据韦达定理,结合向量的模长关系,即可容易求得.
(1)以线段![]() 为直径的圆方程为
为直径的圆方程为![]() ,
,
因为其与直线![]() 相切,
相切,
故可得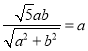 ,
,
又![]() 满足椭圆方程,故可得
满足椭圆方程,故可得![]() ,
,
故可得![]() ,
,
故可得椭圆方程为![]() .
.
(2)因为![]() ,故可得
,故可得![]() ,
,
设![]() 坐标分别为
坐标分别为![]() ,即
,即![]() ;
;
设直线方程为![]() ,
,
联立椭圆方程可得![]() ,
,
若要使得直线与椭圆交于两点,
则![]() ,
,
解得![]() ,即
,即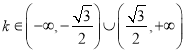 .
.
故可得![]() ,
,
则![]()
![]() .
.
要满足题意,只需![]() ,
,
即![]() ,则
,则![]() .
.
综上所述: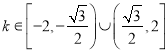 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某中学为了解中学生的课外阅读时间,决定在该中学的1200名男生和800名女生中按分层抽样的方法抽取20名学生,对他们的课外阅读时间进行问卷调查。现在按课外阅读时间的情况将学生分成三类:A类(不参加课外阅读),B类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),C类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时)。调查结果如下表:
A类 | B类 | C类 | |
男生 | x | 5 | 3 |
女生 | y | 3 | 3 |
(I)求出表中x,y的值;
(II)根据表中的统计数据,完成下面的列联表,并判断是否有90%的把握认为“参加课外阅读与否”与性别有关;
男生 | 女生 | 总计 | |
不参加课外阅读 | |||
参加课外阅读 | |||
总计 |
(III)从抽出的女生中再随机抽取3人进一步了解情况,记X为抽取的这3名女生中A类人数和C类人数差的绝对值,求X的数学期望。
附:K2=![]() )
)
P(K2≥k0) | 0.10 | 0.01 | |
k0 | 2.706 | 3.841 | 6.635 |

