Question

【题目】某港口有一个泊位，现统计了某100艘轮船在该泊位停靠的时间（单位：小时），如果停靠时间不足半小时按半小时计时，超过半小时不足1小时按1小时计时，以此类推，统计结果如下表：

（1）设该月100艘轮船在该泊位的平均停靠时间为小时，求的值；

（2）假定某天只有甲、乙两艘轮船需要在该泊位停靠小时，且在一昼夜的时间段中随机到达，求这两艘轮船至少有一艘在停靠该泊位时必须等待的概率.

Answer 1

【答案】（1）；（2）.

【解析】

（1）利用总时间除以求得平均停靠时间.（2）设出甲乙两船到达的时间，由（1）列出不等式，画出可行域后，利用面积的比求得需要等待的概率.

解：（1）.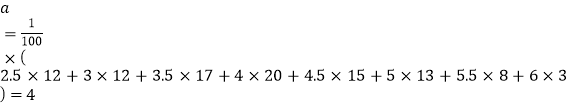

（2）设甲船到达的时间为，乙船到达的时间为，

则

若这两艘轮船在停靠该泊位时至少有一艘需要等待，

则，

符合题意的区域为阴影部分（不包括，轴），

记“这两艘船在停靠该泊位时至少有一艘船需要等待”为事件，

则.

答：这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率为.