题目内容
【题目】折纸是一项艺术,可以折出很多数学图形.将一张圆形纸片放在平面直角坐标系中,圆心B(-1,0),半径为4,圆内一点A为抛物线![]() 的焦点.若每次将纸片折起一角,使折起部分的圆弧的一点
的焦点.若每次将纸片折起一角,使折起部分的圆弧的一点![]() 始终与点A重合,将纸展平,得到一条折痕,设折痕与线段
始终与点A重合,将纸展平,得到一条折痕,设折痕与线段![]() B的交点为P.
B的交点为P.
(Ⅰ)将纸片展平后,求点P的轨迹C的方程;
(Ⅱ)已知过点A的直线l与轨迹C交于R,S两点,当l无论如何变动,在AB所在直线上存在一点T,使得![]() 所在直线一定经过原点,求点T的坐标.
所在直线一定经过原点,求点T的坐标.
【答案】(Ⅰ)轨迹C的方程为![]() ;(Ⅱ)点T的坐标为(4,0).
;(Ⅱ)点T的坐标为(4,0).
【解析】
(Ⅰ)依题意知PA=P![]() ,P的轨迹是以B、A为焦点,长轴长为4,焦距为2的椭圆,由题意能求出其椭圆方程;(Ⅱ)题意等价于在AB所在直线上存在一点T,使得TS与TR所在直线关于x轴对称,当直线l垂直于x轴时,x轴上任意一点都满足TS与TR所在直线关于x轴对称,当直线l不垂直于x轴时,假设存在T(t,0)满足条件,设l的方程为y=k(x﹣1),R(x1,y1),S(x2,y2),联立
,P的轨迹是以B、A为焦点,长轴长为4,焦距为2的椭圆,由题意能求出其椭圆方程;(Ⅱ)题意等价于在AB所在直线上存在一点T,使得TS与TR所在直线关于x轴对称,当直线l垂直于x轴时,x轴上任意一点都满足TS与TR所在直线关于x轴对称,当直线l不垂直于x轴时,假设存在T(t,0)满足条件,设l的方程为y=k(x﹣1),R(x1,y1),S(x2,y2),联立![]() ,得(3+4k2)x2﹣8k2x+4k2﹣12=0,由此利用根与系数的关系、根的判别式、直线关于x轴对称,结合已知条件能求出存在T(4,0),使得当l变化时,总有TS与TR所在直线关于x轴对称.
,得(3+4k2)x2﹣8k2x+4k2﹣12=0,由此利用根与系数的关系、根的判别式、直线关于x轴对称,结合已知条件能求出存在T(4,0),使得当l变化时,总有TS与TR所在直线关于x轴对称.
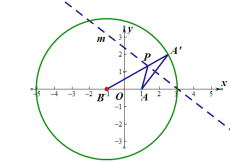
(Ⅰ)依题意:折痕所在直线m为线段![]() 的垂直平分线,∴PA=P
的垂直平分线,∴PA=P![]() ,
,
∴PB+PA= PB + P![]() =4>2,
=4>2,
∴P的轨迹是以B、A为焦点,长轴长为4,焦距为2的椭圆.
∴b2=3.
∴椭圆方程为![]() .
.
(Ⅱ)由题意可知:在AB所在直线上存在一点T,使得![]() 所在直线一定经过原点等价于在AB所在直线上存在一点T,使得TS与TR所在直线关于x轴对称
所在直线一定经过原点等价于在AB所在直线上存在一点T,使得TS与TR所在直线关于x轴对称
当直线l垂直于x轴时,x轴上任意一点都满足TS与TR所在直线关于x轴对称,
当直线l不垂直于x轴时,假设存在T(t,0)满足条件,
设l的方程为y=k(x﹣1),R(x1,y1),S(x2,y2),
联立![]() ,得(3+4k2)x2﹣8k2x+4k2﹣12=0,
,得(3+4k2)x2﹣8k2x+4k2﹣12=0,
由根与系数的关系得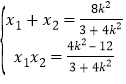 ,①,其中△>0,
,①,其中△>0,
∵TS与TR所在直线关于x轴对称,∴![]() =0,②
=0,②
∵R,S两点在直线y=k(x﹣1)上,
∴y1=k(x1﹣1),y2=k(x2﹣1),代入②,得:
![]() =
=![]() =0,
=0,
∴2x1x2﹣(t+1)(x1+x2)+2t=0,③
将①代入③,得![]() =
=![]() =0,④
=0,④
要使得④与k的取值无关,则t=4,
综上所述,存在T(4,0),使得当l变化时,总有TS与TR所在直线关于x轴对称,即在AB所在直线上存在一点T,使得![]() 所在直线一定经过原点.
所在直线一定经过原点.

 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案