题目内容
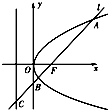
已知抛物线y2=2px(p>0),焦点为F,一直线l与抛物线交于A、B两点,且|AF|+|BF|=8,且AB的垂直平分线恒过定点S(6,0)
①求抛物线方程;
②求△ABS面积的最大值.
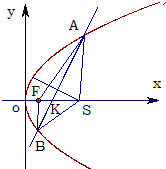
①求抛物线方程;
②求△ABS面积的最大值.

①设A(x1,y1),B(x2,y2),AB中点M(x0,y0)
当直线的斜率存在时,设斜率为k,则由|AF|+|BF|=8得x1+x2+p=8,∴x0=4-
又
得
-
=2p(x1-x2),∴y0=
所以M(4-
,
)
依题意
•k=-1,∴p=4
∴抛物线方程为y2=8x----(6分)
当直线的斜率不存在时,2p=8,也满足上式,∴抛物线方程为y2=8x
②当直线的斜率存在时,由M(2,y0)及kl=
,lAB:y-y0=
(x-2)
令y=0,得xK=2-
又由y2=8x和lAB:y-y0=
(x-2)得:y2-2y0y+2
-16=0
∴S△ABS=
≤
•
=
----(12分)
当直线的斜率不存在时,AB的方程为x=2,|AB|=8,△ABS面积为
×8×4=16
∵
>16,∴△ABS面积的最大值为
.
当直线的斜率存在时,设斜率为k,则由|AF|+|BF|=8得x1+x2+p=8,∴x0=4-
| p |
| 2 |
又
|
| y | 21 |
| y | 22 |
| p |
| k |
所以M(4-
| p |
| 2 |
| p |
| k |
依题意
| ||
4-
|
∴抛物线方程为y2=8x----(6分)
当直线的斜率不存在时,2p=8,也满足上式,∴抛物线方程为y2=8x
②当直线的斜率存在时,由M(2,y0)及kl=
| 4 |
| y0 |
| 4 |
| y0 |
令y=0,得xK=2-
| 1 |
| 4 |
| y | 20 |
又由y2=8x和lAB:y-y0=
| 4 |
| y0 |
| y | 20 |
∴S△ABS=
| ||
| 8 |
| (16+y02)2(32-2y02) |
| ||
| 8 |
(
|
64
| ||
| 9 |
当直线的斜率不存在时,AB的方程为x=2,|AB|=8,△ABS面积为
| 1 |
| 2 |
∵
64
| ||
| 9 |
64
| ||
| 9 |

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
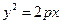 的焦点
的焦点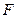 作一直线,和抛物线相交于
作一直线,和抛物线相交于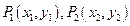 ,求
,求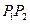 的长。
的长。