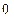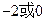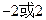题目内容
经过抛物线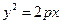 的焦点
的焦点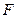 作一直线,和抛物线相交于
作一直线,和抛物线相交于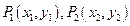 ,求
,求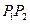 的长。
的长。
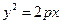 的焦点
的焦点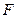 作一直线,和抛物线相交于
作一直线,和抛物线相交于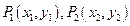 ,求
,求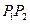 的长。
的长。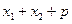
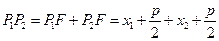
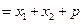 。
。名师点金:原题中的焦点弦是垂直于对称轴的,这样的焦点弦称为通径,它的长为
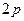 ,变成任一条焦点弦后,利用抛物线的定义可得
,变成任一条焦点弦后,利用抛物线的定义可得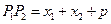 ,事实上,原题是变式的一种特殊情况:即
,事实上,原题是变式的一种特殊情况:即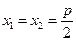 时,
时,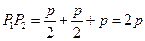 。另外,此题还可以变成:过焦点
。另外,此题还可以变成:过焦点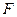 作一倾角为
作一倾角为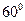 的直线
的直线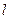 交抛物线于
交抛物线于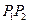 两点,求
两点,求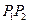 的长,此时
的长,此时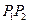 的长仍然为
的长仍然为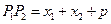 ,但要把直线的方程与抛物线的方程联立后,消去
,但要把直线的方程与抛物线的方程联立后,消去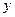 得关于
得关于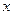 的一元二次方程,从而利用韦达定理得到
的一元二次方程,从而利用韦达定理得到 ,最后得到
,最后得到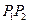 的长。
的长。
练习册系列答案
相关题目
 过定点A(4,0)且与抛物线
过定点A(4,0)且与抛物线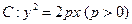 交于P、Q两点,若以PQ为直径的圆恒过原点O,求
交于P、Q两点,若以PQ为直径的圆恒过原点O,求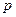 的值。
的值。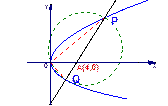
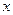 轴为对称轴,焦点在直线
轴为对称轴,焦点在直线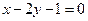 上.
上.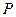 是抛物线上一点,点
是抛物线上一点,点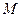 的坐标为
的坐标为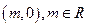 ,求
,求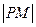 的最小值(用
的最小值(用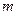 表示),并指出此时点
表示),并指出此时点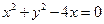 的圆心,(1)求抛物线的方程;(2)直线
的圆心,(1)求抛物线的方程;(2)直线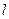 的斜率为
的斜率为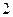 ,且过抛物线的焦点,若
,且过抛物线的焦点,若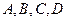 四个点,求
四个点,求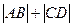 。
。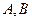 是抛物线
是抛物线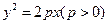 上两点,
上两点,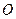 为坐标原点,若
为坐标原点,若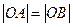 ,且
,且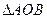 的垂心恰是此抛物线的焦点,则直线
的垂心恰是此抛物线的焦点,则直线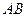 的方程是( )
的方程是( )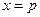
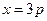
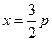
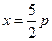
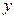 轴上的抛物线上的一点
轴上的抛物线上的一点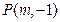 到焦点的距离为
到焦点的距离为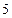 ,则
,则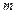 的值为( )
的值为( )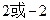
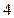
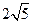
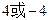
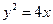 上一动点,点P到直线
上一动点,点P到直线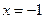 的距离为
的距离为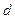 ,则
,则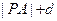 的最小值为
的最小值为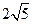
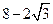
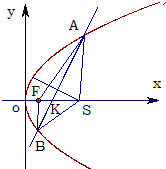
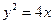 上一点,点B的坐标为
上一点,点B的坐标为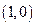 ,且
,且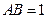 ,则点
,则点 的横坐标的值为( )
的横坐标的值为( )