题目内容
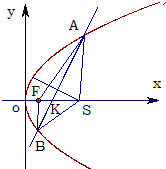
过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B(如图所示),交其准线于点C,若|BC|=2|BF|,且|AF|=4,则此抛物线的方程为( )
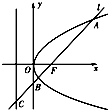
| A.y2=8x | B.y2=4x | C.y2=2x | D.y2=
|

如图过A作AD垂直于抛物线的准线,垂足为D,
过B作BE垂直于抛物线的准线,垂足为E,P为准线与x轴的焦点,
由抛物线的定义,|BF|=|BE|,|AF|=|AD|=4,
∵|BC|=2|BF|,∴|BC|=2|BE|,∴∠DCA=30°
∴|AC|=2|AD|=8,∴|CF|=8-4=4,
∴|PF|=
=2,即p=|PF|=2,
∴所以抛物线方程为:y2=4x,
故选B

过B作BE垂直于抛物线的准线,垂足为E,P为准线与x轴的焦点,
由抛物线的定义,|BF|=|BE|,|AF|=|AD|=4,
∵|BC|=2|BF|,∴|BC|=2|BE|,∴∠DCA=30°
∴|AC|=2|AD|=8,∴|CF|=8-4=4,
∴|PF|=
| |CF| |
| 2 |
∴所以抛物线方程为:y2=4x,
故选B


练习册系列答案
相关题目
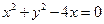 的圆心,(1)求抛物线的方程;(2)直线
的圆心,(1)求抛物线的方程;(2)直线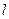 的斜率为
的斜率为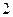 ,且过抛物线的焦点,若
,且过抛物线的焦点,若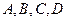 四个点,求
四个点,求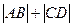 。
。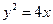 上一动点,点P到直线
上一动点,点P到直线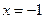 的距离为
的距离为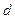 ,则
,则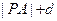 的最小值为
的最小值为