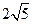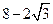题目内容
已知抛物线C的顶点为原点,其焦点F(0,c)(c>0)到直线l:x-y-2=0的距离为
,设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.
(1)求抛物线C的方程;
(2)当点P(x0,y0)为直线l上的定点时,求直线AB的方程;
(3)当点P在直线l上移动时,求|AF|•|BF|的最小值.
3
| ||
| 2 |
(1)求抛物线C的方程;
(2)当点P(x0,y0)为直线l上的定点时,求直线AB的方程;
(3)当点P在直线l上移动时,求|AF|•|BF|的最小值.
(1)焦点F(0,c)(c>0)到直线l:x-y-2=0的距离d=
=
=
,解得c=1
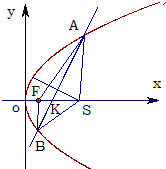
所以抛物线C的方程为x2=4y
(2)设A(x1,
),B(x2,
)
由(1)得抛物线C的方程为y=
x2,y′=
x,所以切线PA,PB的斜率分别为
x1,
x2
所以PA:y-
=
x1(x-x1)①PB:y-
=
x2(x-x2)②
联立①②可得点P的坐标为(
,
),即x0=
,y0=
又因为切线PA的斜率为
x1=
,整理得y0=
x1x0-
直线AB的斜率k=
=
=
所以直线AB的方程为y-
=
x0(x-x1)
整理得y=
x0x-
x1x0+
,即y=
x0x-y0
因为点P(x0,y0)为直线l:x-y-2=0上的点,所以x0-y0-2=0,即y0=x0-2
所以直线AB的方程为y=
x0x-x0+2
(3)根据抛物线的定义,有|AF|=
+1,|BF|=
+1
所以|AF|•|BF|=(
+1)(
+1)=
+
(
+
)+1=
+
[(x1+x2)2-2x1x2]+1
由(2)得x1+x2=2x0,x1x2=4y0,x0=y0+2
所以|AF|•|BF|=
+
(4
-8y0)+1=
+
-2y0+1=(y0+2)2+
-2y0+1=2
+2y0+5=2(y0+
)2+
所以当y0=-
时,|AF|•|BF|的最小值为
| |-c-2| | ||
|
| c+2 | ||
|
3
| ||
| 2 |
所以抛物线C的方程为x2=4y
(2)设A(x1,
| 1 |
| 4 |
| x | 21 |
| 1 |
| 4 |
| x | 22 |
由(1)得抛物线C的方程为y=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以PA:y-
| 1 |
| 4 |
| x | 21 |
| 1 |
| 2 |
| 1 |
| 4 |
| x | 22 |
| 1 |
| 2 |
联立①②可得点P的坐标为(
| x1+x2 |
| 2 |
| x1x2 |
| 4 |
| x1+x2 |
| 2 |
| x1x2 |
| 4 |
又因为切线PA的斜率为
| 1 |
| 2 |
y0-
| ||||
| x0-x1 |
| 1 |
| 2 |
| 1 |
| 4 |
| x | 21 |
直线AB的斜率k=
| ||||||||
| x1-x2 |
| x1+x2 |
| 4 |
| x0 |
| 2 |
所以直线AB的方程为y-
| 1 |
| 4 |
| x | 21 |
| 1 |
| 2 |
整理得y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| x | 21 |
| 1 |
| 2 |
因为点P(x0,y0)为直线l:x-y-2=0上的点,所以x0-y0-2=0,即y0=x0-2
所以直线AB的方程为y=
| 1 |
| 2 |
(3)根据抛物线的定义,有|AF|=
| 1 |
| 4 |
| x | 21 |
| 1 |
| 4 |
| x | 22 |
所以|AF|•|BF|=(
| 1 |
| 4 |
| x | 21 |
| 1 |
| 4 |
| x | 22 |
| 1 |
| 16 |
| x | 21 |
| x | 22 |
| 1 |
| 4 |
| x | 21 |
| x | 22 |
| 1 |
| 16 |
| x | 21 |
| x | 22 |
| 1 |
| 4 |
由(2)得x1+x2=2x0,x1x2=4y0,x0=y0+2
所以|AF|•|BF|=
| y | 20 |
| 1 |
| 4 |
| x | 20 |
| x | 20 |
| y | 20 |
| y | 20 |
| y | 20 |
| 1 |
| 2 |
| 9 |
| 2 |
所以当y0=-
| 1 |
| 2 |
| 9 |
| 2 |

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
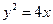 上一动点,点P到直线
上一动点,点P到直线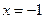 的距离为
的距离为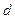 ,则
,则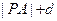 的最小值为
的最小值为