题目内容
已知双曲线方程为
-
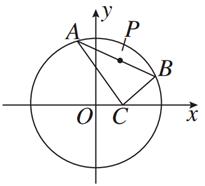
=1(a>0,b>0),右焦点为F,点A(0,b),线段AF交双曲线于点B,且
=2
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| AB |
| BF |
A.
| B.
| C.
| D.
|
设B(x,y),
∵右焦点为F,点A(0,b),线段AF交双曲线于点B,且
=2
,
∴(x,y-b)=2(c-x,-y),
∴x=
,y=
,
代入双曲线方程,可得
-
=1,
∴
=
.
故选A.
∵右焦点为F,点A(0,b),线段AF交双曲线于点B,且
| AB |
| BF |
∴(x,y-b)=2(c-x,-y),
∴x=
| 2c |
| 3 |
| b |
| 3 |
代入双曲线方程,可得
| ||
| a2 |
| ||
| b2 |
∴
| c |
| a |
| ||
| 2 |
故选A.

练习册系列答案
相关题目
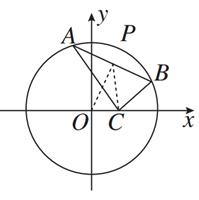
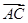 ·
· =0,设P为弦AB的中点.
=0,设P为弦AB的中点.