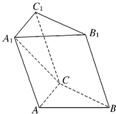
题目内容
如图,在三棱柱ABC-A1B1C1中,AB=
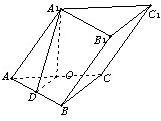
a,BC=CA=AA1=a,且A1O⊥平面ABC,点O在AC上且为AC中点,求此三棱柱的侧面积.
| 2 |

因为O为AC中点,AA1=AC=a,所以AO=
a,A1O=
a,
SAA1CC1=a•
a=
a2,因为BC⊥平面A1C,所以BC⊥CC1,
所以侧面BCC1B1为矩形,所以S?BCC1B1=a•a=a2,
过O作OD⊥AB于D,连接A1D,因为A1O⊥平面ABC,所以A1D⊥AB,
因为OD=AO•sin45°=
a,所以A1D=
=
a,
所以S平行四边形ABB1A1=
a•
a=
a2,所以S侧 =
(2+
+
)a2.
| 1 |
| 2 |
| ||
| 2 |
SAA1CC1=a•
| ||
| 2 |
| ||
| 2 |
所以侧面BCC1B1为矩形,所以S?BCC1B1=a•a=a2,
过O作OD⊥AB于D,连接A1D,因为A1O⊥平面ABC,所以A1D⊥AB,
因为OD=AO•sin45°=
| ||
| 4 |
| A1O2+OD2 |
| ||
| 4 |
所以S平行四边形ABB1A1=
| 2 |
| ||
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 7 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,