题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为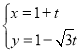 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,设
两点,设![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)在曲线![]() 的极坐标方程中,由
的极坐标方程中,由![]() ,
,![]() 可将曲线
可将曲线![]() 的极坐标方程化为直角坐标方程,在直线
的极坐标方程化为直角坐标方程,在直线![]() 的参数方程中消去参数
的参数方程中消去参数![]() ,可得出直线
,可得出直线![]() 的普通方程;
的普通方程;
(2)将直线![]() 的参数方程表示为
的参数方程表示为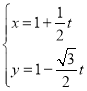 (
(![]() 为参数),并设点
为参数),并设点![]() 、
、![]() 对应的参数分别为
对应的参数分别为![]() 、
、![]() ,将直线
,将直线![]() 的参数方程与曲线
的参数方程与曲线![]() 的普通方程联立,得出关于
的普通方程联立,得出关于![]() 的二次方程,并列出韦达定理,可计算出
的二次方程,并列出韦达定理,可计算出![]() 的值.
的值.
(1)在曲线![]() 的极坐标方程中,由
的极坐标方程中,由![]() ,
,![]() 可得出曲线
可得出曲线![]() 的普通方程为
的普通方程为![]() ,即
,即![]() .
.
在直线![]() 的参数方程中消去
的参数方程中消去![]() 得
得![]() ,即
,即![]() ;
;
(2)直线![]() 的参数方程表示为
的参数方程表示为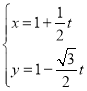 (
(![]() 为参数),
为参数),
并设点![]() 、
、![]() 对应的参数分别为
对应的参数分别为![]() 、
、![]() ,
,
将直线![]() 的参数方程与曲线
的参数方程与曲线![]() 的直角坐标方程联立,消去
的直角坐标方程联立,消去![]() 、
、![]() 得
得![]() .
.
由韦达定理得![]() ,
,![]() .
.
因此,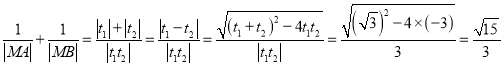 .
.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
【题目】某企业为了检查生产![]() 产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在
产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.下表是甲流水线样本的频数分布表,下图是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.下表是甲流水线样本的频数分布表,下图是乙流水线样本的频率分布直方图.
甲流水线样本的频数分布表
质量指标值 | 频数 |
| 9 |
| 10 |
| 17 |
| 8 |
| 6 |
乙流水线样本的频率分布直方图
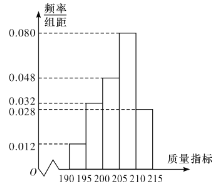
(1)根据图形,估计乙流水线生产的![]() 产品的该项质量指标值的中位数;
产品的该项质量指标值的中位数;
(2)设该企业生产一件合格品获利100元,生产一件不合格品亏损50元,若某个月内甲、乙两条流水线均生产了1000件产品,若将频率视为概率,则该企业本月的利润约为多少元?