题目内容
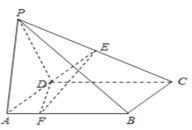
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,且![]() ,平面PCD⊥平面ABCD,
,平面PCD⊥平面ABCD,![]() ,点E为线段PC的中点,点F是线段AB上的一个动点.
,点E为线段PC的中点,点F是线段AB上的一个动点.
(1)求证:平面![]() 平面PBC;
平面PBC;
(2)设二面角![]() 的平面角为
的平面角为![]() ,试判断在线段AB上是否存在这样的点F,使得
,试判断在线段AB上是否存在这样的点F,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)证明见解析(2)存在;![]()
【解析】
(1)根据平面与平面垂直的性质易知![]() 平面
平面![]() ,从而
,从而![]() ,由三线合一易证
,由三线合一易证![]() ,从而
,从而![]() 平面
平面![]() ,即可由面面垂直的判定定理证明平面
,即可由面面垂直的判定定理证明平面![]() 平面PBC;
平面PBC;
(2)在平面![]() 内过
内过![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为原点,以
为原点,以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,建立空间直角坐标系,写出各个点的坐标,并由题意设
轴,建立空间直角坐标系,写出各个点的坐标,并由题意设![]() ,表示出平面
,表示出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量.根据同角三角函数关系式可由
的法向量.根据同角三角函数关系式可由![]() 求得
求得![]() ,结合空间向量夹角运算求得
,结合空间向量夹角运算求得![]() 的值,进而确定
的值,进而确定![]() 的值.
的值.
(1)![]() 四边形
四边形![]() 是正方形,
是正方形,
∴![]() .
.
∵平面![]()
![]() 平面
平面![]() 平面
平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() .
.
∵![]() ,点
,点![]() 为线段
为线段![]() 的中点,
的中点,
∴![]() .
.
又∵![]() ,
,
∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,
,
∴平面![]()
![]() 平面
平面![]() .
.
(2)由(1)知![]() 平面
平面![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() .
.
在平面![]() 内过
内过![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
∴![]() ,故
,故![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为原点,
为原点,
以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,建立如图所示空间直角坐标系
轴,建立如图所示空间直角坐标系![]() .
.
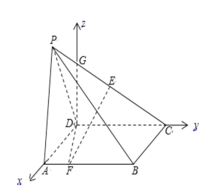
因为![]() ,
,
![]() ,∴
,∴![]() .
.
∵![]() 平面
平面![]() ,则
,则![]() ,
,![]() ,
,![]()
又![]() 为
为![]() 的中点,
的中点,![]() ,假设在线段
,假设在线段![]() 上存在这样的点
上存在这样的点![]() ,使得
,使得![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则
∴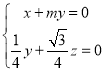 ,令
,令![]() ,则
,则![]()
![]() ,则
,则![]()
![]()
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 的一个法向量
的一个法向量![]() ,
,![]() ,则
,则![]()
∴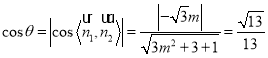 .
.
![]() ,解得
,解得![]() ,
,
∴![]()

 中考解读考点精练系列答案
中考解读考点精练系列答案【题目】一般来说,一个人脚掌越长,他的身高就越高.现对10名成年人的脚掌长![]() 与身高
与身高![]() 进行测量,得到数据(单位均为
进行测量,得到数据(单位均为![]() )作为样本如下表所示.
)作为样本如下表所示.
脚掌长(x) | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
身高(y) | 141 | 146 | 154 | 160 | 169 | 176 | 181 | 188 | 197 | 203 |
(1)在上表数据中,以“脚掌长”为横坐标,“身高”为纵坐标,作出散点图后,发现散点在一条直线附近,试求“身高”与“脚掌长”之间的线性回归方程![]() ;
;
(2)若某人的脚掌长为![]() ,试估计此人的身高;
,试估计此人的身高;
(3)在样本中,从身高180cm以上的4人中随机抽取2人作进一步的分析,求所抽取的2人中至少有1人身高在190cm以上的概率.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)