题目内容
【题目】已知函数![]()
![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(Ⅱ)若函数![]() 有两个不同零点
有两个不同零点![]() ,
, ![]() ,且
,且![]() ,求证:
,求证: ![]() ,其中
,其中![]() 是
是![]() 的导函数.
的导函数.
【答案】(Ⅰ)y=2x-1;(Ⅱ)证明见解析.
【解析】试题分析:(I)利用导数的几何意义即可得出![]() 的图象在
的图象在![]() 处的切线方程;(Ⅱ)由于
处的切线方程;(Ⅱ)由于![]() 的图象与
的图象与![]() 轴交于两个不同的点
轴交于两个不同的点![]() ,
, ![]() ,可得方程
,可得方程![]() 的两个根为
的两个根为![]() ,
, ![]() ,得到
,得到![]() ,可得
,可得![]() ,经过变形只要证明
,经过变形只要证明![]() ,通过换元再利用导数研究其单调性即可得出.
,通过换元再利用导数研究其单调性即可得出.
试题解析:(Ⅰ)当![]() 时,
时, ![]() ,
, ![]() ,切点坐标为
,切点坐标为![]() ,切线的斜率
,切线的斜率![]() ,∴切线方程为
,∴切线方程为![]() ,即
,即![]() .
.
(Ⅱ)∵![]() 的图象与
的图象与![]() 轴交于两个不同的点
轴交于两个不同的点![]() ,
, ![]() ,∴方程
,∴方程![]() 的两个根为
的两个根为![]() ,
, ![]() ,则
,则![]() ,两式相减得
,两式相减得![]() ,又
,又![]() ,
, ![]() ,则
,则![]() ,下证
,下证![]() (*),即证明
(*),即证明![]() ,令
,令![]() ,∵
,∵![]() ,∴
,∴![]() ,即证明
,即证明![]() 在
在![]() 上恒成立,∵
上恒成立,∵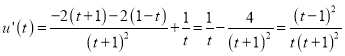 ,又
,又![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上是增函数,则
上是增函数,则![]() ,从而知
,从而知![]() ,故(*)式
,故(*)式![]() ,即
,即![]() 成立.
成立.

练习册系列答案
相关题目
【题目】随着互联网经济逐步被人们接受,网上购物的人群越来越多,网银交易额也逐年增加,某地连续五年的网银交易额统计表,如表所示:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
网银交易额 | 5 | 6 | 7 | 8 | 10 |
经研究发现,年份与网银交易额之间呈线性相关关系,为了计算的方便,工作人员将上表的数据进行了处理,![]() ,
,![]() ,得到如表:
,得到如表:
时间代号 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)通过(1)中的方程,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)用所求回归方程预测2020年该地网银交易额.
(附:在线性回归方程![]() 中,
中,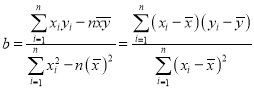 ,
,![]() )
)