题目内容
7.已知函数f(x)=-x2+2|x-a|(a∈R).(1)当a=$\frac{1}{2}$时,求y=f(x)的单调递增区间;
(2)当a>0时,若对任意的x∈[0,+∞),不等式f(x-1)≥2f(x)恒成立,求实数a的取值范围.
分析 (1)去绝对值,讨论二次函数的对称轴和区间的关系,即可得到递增区间;
(2)由题意可得,x∈[0,+∞)时,不等式x2+2x-1+2|x-(a+1)|-4|x-a|≥0恒成立,再分①当0≤x≤a时、②当x≥a+1、③当a<x<a+1时三种情况,分别求得a的范围,再取交集,即为所求.
解答 解:(1)当a=$\frac{1}{2}$时,f(x)=-x2+2|x-$\frac{1}{2}$|,
当x$≥\frac{1}{2}$时,f(x)=-x2+2x-1=-(x-1)2,在($\frac{1}{2}$,1)函数递增;
当x<$\frac{1}{2}$时,f(x)=-x2+1-2x=-(x+1)2+2,在(-∞,-1)函数递增.
即有函数f(x)的单调递增区间为($\frac{1}{2}$,1),(-∞,-1);
(2)由题意可得,x∈[0,+∞)时,不等式x2+2x-1+2|x-(a+1)|-4|x-a|≥0恒成立 ①.
(Ⅰ)当0≤x≤a时,①即 x2+4x-2a+1≥0恒成立,
由于当x=0时,不等式左边取得最小为-2a+1,
再由-2a+1≥0求得 a≤$\frac{1}{2}$,∴0<a≤$\frac{1}{2}$.
(Ⅱ)当x≥a+1,①即x2+2a-3≥0 恒成立,
由于当x=a+1时,不等式的左边取得最小值为a2+4a-2,
再由a2+4a-2≥0求得a≥$\sqrt{6}$-2.
(Ⅲ)当a<x<a+1时,①即 x2-4x+6a+1≥0恒成立,
该不等式对应的二次函数的图象开口向上,对称轴为x=2,
若a>2,则当x=a时,不等式的左边取得最小值为a2+2a+1,
由a2+2a+1≥0,求得a∈R,故此时有 a>2.
若a≤2≤a+1,则当x=2时,不等式的左边取得最小值为6a-3,
由6a-3≥0,求得a≥$\frac{1}{2}$,故此时有1≤a≤2.
若a+1<2,则当x=a+1时,不等式左边取得最小值为a2+4a-2≥0,求得a≥$\sqrt{6}$-2,
故此时有$\sqrt{6}$-2<a<1.
故在此分类条件下,a≥-2+$\sqrt{6}$.
综上可得$\sqrt{6}$-2≤a≤$\frac{1}{2}$,
即a的范围为[$\sqrt{6}$-2,$\frac{1}{2}$].
点评 本题主要考查分段函数的单调区间的求法和二次函数的性质的应用,体现了分类讨论、转化的数学思想,属于中档题.

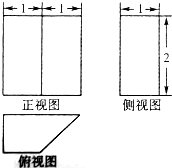
| A. | $\frac{2}{3}$ | B. | 1 | C. | 3 | D. | 6 |
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
| A. | 球 | B. | 三棱锥 | C. | 正方体 | D. | 圆柱 |
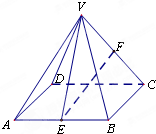 如图所示,在正四棱锥V-ABCD中,AB=4,E、F分别为AB、VC边的中点,直线VE与面VBC所成角为$\frac{π}{6}$.
如图所示,在正四棱锥V-ABCD中,AB=4,E、F分别为AB、VC边的中点,直线VE与面VBC所成角为$\frac{π}{6}$.