题目内容
6.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)经过点$(2,\sqrt{2})$,且离心率为$\frac{{\sqrt{2}}}{2}$.(Ⅰ)求椭圆C的方程;
(Ⅱ)设经过椭圆C左焦点的直线交椭圆于M、N两点,线段MN的垂直平分线交y轴于点P(0,m),求m的取值范围.
分析 (I)由椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)经过点$(2,\sqrt{2})$,且离心率为$\frac{{\sqrt{2}}}{2}$,可得$\frac{4}{{a}^{2}}+\frac{2}{{b}^{2}}=1$,$\frac{c}{a}=\frac{\sqrt{2}}{2}$,又a2=b2+c2,联立解得即可.
(II)当直线MN⊥x轴时,线段MN的垂直平分线为x轴,可得m=0.当直线MN的斜率存在时,可设直线MN的方程为y=k(x+2)(k≠0),与椭圆方程联立化为
(1+2k2)x2+8k2x+8k2-8=0,设M(x1,y1),N(x2,y2),线段MN的中点为Q(x0,y0),利用根与系数的关系及其中点坐标公式可得(x0,y0),可得线段MN的垂直平行线的方程,对k分类讨论即可得出.
解答 解:(I)∵椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)经过点$(2,\sqrt{2})$,且离心率为$\frac{{\sqrt{2}}}{2}$,
∴$\frac{4}{{a}^{2}}+\frac{2}{{b}^{2}}=1$,$\frac{c}{a}=\frac{\sqrt{2}}{2}$,又a2=b2+c2,
联立解得b=c=2,a2=8.
∴椭圆C的方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$.
(II)当直线MN⊥x轴时,线段MN的垂直平分线为x轴,∴m=0.
当直线MN的斜率存在时,可设直线MN的方程为y=k(x+2)(k≠0),联立$\left\{\begin{array}{l}{y=k(x+2)}\\{{x}^{2}+2{y}^{2}=8}\end{array}\right.$,
化为(1+2k2)x2+8k2x+8k2-8=0,
设M(x1,y1),N(x2,y2),线段MN的中点为Q(x0,y0),
则x1+x2=$\frac{-8{k}^{2}}{1+2{k}^{2}}$,
∴x0=$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{4{k}^{2}}{1+2{k}^{2}}$,y0=k(x0+2)=$\frac{2k}{1+2{k}^{2}}$,
∴线段MN的垂直平行线的方程为$y-\frac{2k}{1+2{k}^{2}}$=-$\frac{1}{k}$$(x+\frac{4{k}^{2}}{1+2{k}^{2}})$,
令x=0,可得m=y=$\frac{-2k}{1+2{k}^{2}}$=$\frac{-2}{\frac{1}{k}+2k}$,
当k>0时,m≥-$\frac{\sqrt{2}}{2}$,当且仅当k=$\frac{\sqrt{2}}{2}$时取等号;当k<0时,m≤$\frac{\sqrt{2}}{2}$,当且仅当k=-$\frac{\sqrt{2}}{2}$时取等号.
综上可得:m的取值范围是$[-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}]$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、中点坐标公式、线段的垂直平分线方程、基本不等式的性质,考查了推理能力与计算能力,属于难题.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案| A. | A?B | B. | A∩B=B | C. | A∩(∁RB)≠∅ | D. | A∪(∁RB)=R |
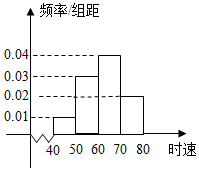 已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,估计这辆汽车在这段公路时速的众数是( )
已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,估计这辆汽车在这段公路时速的众数是( )| A. | 60 | B. | 65 | C. | 60.5 | D. | 70 |
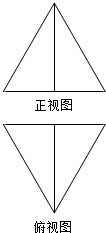
| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
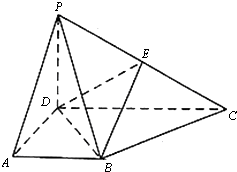 已知四棱锥P-ABCD的底面是直角梯形,AB∥CD,AD⊥AB,AD=AB=$\frac{1}{2}$CD=1,PD⊥面ABCD,PD=$\sqrt{2}$,E是PC的中点
已知四棱锥P-ABCD的底面是直角梯形,AB∥CD,AD⊥AB,AD=AB=$\frac{1}{2}$CD=1,PD⊥面ABCD,PD=$\sqrt{2}$,E是PC的中点