题目内容
15. 如图所示,在正四棱锥V-ABCD中,AB=4,E、F分别为AB、VC边的中点,直线VE与面VBC所成角为$\frac{π}{6}$.
如图所示,在正四棱锥V-ABCD中,AB=4,E、F分别为AB、VC边的中点,直线VE与面VBC所成角为$\frac{π}{6}$.(1)求证:EF∥平面VAD.
(2)求二面角E-VD-B的大小.
分析 (1)根据线面平行的性质定理证明面EFG∥面VAD即可证明EF∥平面VAD.
(2)法一:利用定义法求解二面角E-VD-B的大小.
法二:建立空间坐标系,利用向量法进行求解.
解答 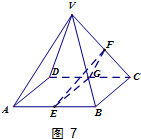 解:(1)如图7取CD的中点G,连结EG,FG.
解:(1)如图7取CD的中点G,连结EG,FG.
∵E,G分别为AB,CD的中点,
∴EG∥AD,FG∥VD.
∵EG?面VAD,AD?面VAD,∴EG∥面VAD…(2分)
同理可得FG∥面VAD
又∵EG∩FG=G,所以面EFG∥面VAD.…(3分)
∵EF?面EFG,∴EF∥面VAD.…(4分)
(2)(法一)过点V作VO⊥面ABCD于O,则由正四棱锥的定义可知O为正方形ABCD的中心.
取BC的中点H,连结OH,VH,则OH=2
设VO=h,则$VH=\sqrt{4+{h^2}}$,设点E到面VBC的距离为h'.
∵${V_{V-BCE}}=\frac{1}{3}{S_{△BCE}}•h=\frac{1}{3}•\frac{1}{2}•2•4•h=\frac{4}{3}h$
又${V_{E-VBC}}=\frac{1}{3}•{S_{△VBC}}•h'=\frac{1}{3}•\frac{1}{2}•4•\sqrt{4+{h^2}}•h'=\frac{2}{3}\sqrt{4+{h^2}}•h'$
由VV-BCE=VE-VBC得$h'=\frac{2h}{{\sqrt{4+{h^2}}}}$…7分
∵直线VE与面VBC所成角为$\frac{π}{6}$,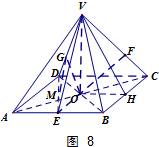
设直线VE与面VBC所成角为θ,
则$sinθ=\frac{h'}{VE}=\frac{2h}{{VE•\sqrt{4+{h^2}}}}=\frac{1}{2}$…(8分)
∵$VE=VH=\sqrt{4+{h^2}}$,故有$\frac{2h}{{\sqrt{4+{h^2}}•\sqrt{4+{h^2}}}}=\frac{1}{2}$,解得h=2.…(9分)
过O作OG⊥VD于G,连结DE交AC于M,连结GM.
∵VO⊥面ABCD,AC?面ABCD,故VO⊥AC
又∵AC⊥BD,VO∩BD=O,∴AC⊥面VBD…(10分)
∵VD?面VBD,∴AC⊥VD
∵OG⊥VD,OG∩AC=O
∴VD⊥面OGM,故VD⊥GM
∴∠OGM为二面角B-VD-E的平面角.…(11分)
由条件可知$VD=2\sqrt{3}$,故$OG=\frac{OD•OV}{VD}=\frac{{2\sqrt{6}}}{3}$…(12分)
在Rt△ABG中,$sin∠ADE=\frac{{2\sqrt{5}}}{5},cos∠ADE=\frac{{\sqrt{5}}}{5}$
故$sin∠AMD=sin({π-∠ADM-∠DAM})=sin({∠ADM+∠DAM})=\frac{{3\sqrt{10}}}{10}$
在△ADM中,由正弦定理有$DM=\frac{AD•sin∠DAM}{sin∠AMD}=\frac{{4\sqrt{5}}}{3}$.
所以,在Rt△MDO中,$MO=\sqrt{D{M^2}-D{O^2}}=\frac{{2\sqrt{2}}}{3}$…(13分)
∴$tan∠OGM=\frac{OH}{OG}=\frac{{\sqrt{3}}}{3}$,
故所求的二面角B-VD-E的大小为$\frac{π}{6}$.…(14分)
(法二:向量法)
以O为坐标原点,OE,OH,OV所在直线为x,y,z轴建立空间直角坐标系.
则B(2,2,0),C(-2,2,0),E(2,0,0),D(-2,-2,0),V(0,0,h)…(5分)
设面VBC的一个法向量为$\overrightarrow m=({x,y,z})$,则
由$\left\{{\begin{array}{l}{\overrightarrow m•\overrightarrow{BC}=0}\\{\overrightarrow m•\overrightarrow{VB}=0}\end{array}}\right.$得$\left\{{\begin{array}{l}{-4x=0}\\{2x+2y-hz=0}\end{array}}\right.$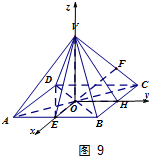
取y=h,则x=0,z=2
故面VBC的一个法向量为$\overrightarrow m=({0,h,2})$…(7分)
∵$\overrightarrow{VE}=({2,0,-h})$,设$\overrightarrow{VE}$与面VBC所成角为$\frac{π}{6}$
则$sin\frac{π}{6}=|{cos\left?{\overrightarrow{VE},\overrightarrow m}\right>}|=\frac{1}{2}$
即$\frac{2h}{{\sqrt{{h^2}+4}•\sqrt{{h^2}+4}}}=\frac{1}{2}$,解得h=2…(9分)
∵VO⊥AC,AC⊥BD,VO∩BD=O,
故AC⊥面VBD,
故面VBD的一个法向量为$\overrightarrow{OA}=({2,-2,0})$…(11分)
设面EVD的一个法向量为$\overrightarrow n=({x,y,z})$
由$\left\{{\begin{array}{l}{\overrightarrow n•\overrightarrow{DE}=0}\\{\overrightarrow n•\overrightarrow{DV}=0}\end{array}}\right.$得$\left\{{\begin{array}{l}{4x+2y=0}\\{2x+2y+2z=0}\end{array}}\right.$,取x=1,则y=-2,z=1,
∴$\overrightarrow n=({1,-2,1})$…(13分)
设二面角E-VD-B的大小为φ,
则$cosφ=|{cos\left?{\overrightarrow{OA},\overrightarrow n}\right>}|=\frac{6}{{2\sqrt{2}•\sqrt{6}}}=\frac{{\sqrt{3}}}{2}$
故$φ=\frac{π}{6}$.…(14分)
点评 本题主要考查线面平行的判断以及二面角的求解,利用定义法或者建立空间坐标系利用向量法是求二面角的常用方法,考查学生的运算和推理能力.

| A. | A?B | B. | A∩B=B | C. | A∩(∁RB)≠∅ | D. | A∪(∁RB)=R |
| A. | x=$\frac{2}{e}$为f(x)的极小值点 | B. | x=$\frac{2}{e}$为f(x)的极大值点 | ||
| C. | x=ln2为f(x)的极小值点 | D. | x=ln2为f(x)的极大值点 |
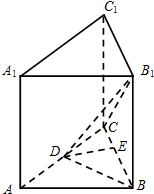 如图,直三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,D为AC中点,E为BC上一点,且∠CDE=∠ABC.
如图,直三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,D为AC中点,E为BC上一点,且∠CDE=∠ABC.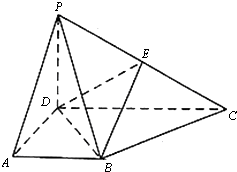 已知四棱锥P-ABCD的底面是直角梯形,AB∥CD,AD⊥AB,AD=AB=$\frac{1}{2}$CD=1,PD⊥面ABCD,PD=$\sqrt{2}$,E是PC的中点
已知四棱锥P-ABCD的底面是直角梯形,AB∥CD,AD⊥AB,AD=AB=$\frac{1}{2}$CD=1,PD⊥面ABCD,PD=$\sqrt{2}$,E是PC的中点