题目内容
8．
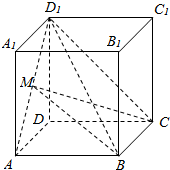如图，已知正方体ABCD-A1B1ClD1的棱长为a，点M为线段AD1的中点．三棱锥D1-BMC的正视图面积等于（ ）| A． | $\frac{1}{2}$a2 | B． | $\frac{1}{4}$a2 | C． | $\frac{\sqrt{2}{a}^{2}}{4}$ | D． | $\frac{\sqrt{3}{a}^{2}}{4}$ |
分析 画出三棱锥D1-BMC的正视图，代入三角形面积公式，可得答案．
解答 解：三棱锥D1-BMC的正视图如下图所示：
由已知中正方体ABCD-A1B1ClD1的棱长为a，
故三棱锥D1-BMC的正视图面积S=$\frac{1}{2}×\frac{a}{2}×a=\frac{1}{4}{a}^{2}$，
故选：B
点评 本题考查的知识点是简单空间图形的三视图，难度不大，属于基础题．
练习册系列答案
百年学典课时学练测系列答案
相关题目
19．已知集合A={x|1og2x＜2}，B=$\left\{{x|\frac{1}{3}＜{3^x}＜\sqrt{3}}\right\}$，则A∪B是（ ）
| A． | $（0，\frac{1}{2}）$ | B． | （0，4] | C． | （-∞，-1]∪（4，+∞） | D． | （-1，4）?? |
20．在正方体ABCD-A1B1C1D1中，异面直线AC与BC1所成角的大小是（ ）
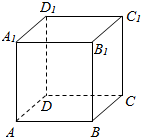
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
17．若关于x的方程2sin（2x+$\frac{π}{6}$）+a-1=0（a∈R）在区间[0，$\frac{π}{2}$]上有两个不相等的实根x1，x2，则（ ）
| A． | x1+x2＞|a+1|1.1 | |
| B． | x1+x2＜|a+1|1.1 | |
| C． | x1+x2=|a+1|1.1 | |
| D． | x1+x2与|a+1|1.1的大小关系无法确定 |
18．在区间〔-1，1〕上随机取一个数x，使sin$\frac{πx}{2}$的值介于0到$\frac{1}{2}$之间的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{3π}$ | D． | $\frac{1}{6π}$ |