题目内容
18.△ABC中,a,b,c分别是A,B,C所对的边,S是该三角形的面积,若bcosC=(2a-c)cosB.(Ⅰ)求∠B的大小;
(Ⅱ)若a=4,S=5$\sqrt{3}$,求b的值.
分析 (1)由已知及正弦定理得:sinBcosC=(2sinA-sinC)cosB,利用三角函数恒等变换的应用可得$cosB=\frac{1}{2}$,结合范围0<B<π,可求B的值.
(2)利用三角形面积公式可求c的值,由余弦定理即可求b的值.
解答 解:(1)由正弦定理得:sinBcosC=(2sinA-sinC)cosB,
∴sinBcosC+sinCcosB=2sinAcosB,
∴sin(B+C)=2sinAcosB,
∵A+B+C=π,
∴sin(B+C)=sinA,
∴$cosB=\frac{1}{2}$,
∵0<B<π,
∴$B=\frac{π}{3}$.
(2)∵△ABC中,${S_△}=\frac{1}{2}acsinB=\frac{1}{2}•4•c•\frac{{\sqrt{3}}}{2}=5\sqrt{3}$,
∴c=5,
∵由余弦定理得:b2=a2+c2-2accosB=16+25-2×4×5×$\frac{1}{2}$=21,
∴$b=\sqrt{21}$.
点评 本题主要考查了三角函数恒等变换的应用,正弦定理,余弦定理,三角形面积公式的应用,属于基本知识的考查.

练习册系列答案
相关题目
13.某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
若单科成绩在85分以上(含85分),则该科成绩为优秀.
(1)根据上表完成下面的2×2列联表(单位:人):
(2)根据题(1)中表格的数据计算,能否有99%的把握认为学生的数学成绩与物理成绩之间有关系?
附:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数学/分 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 |
| 物理/分 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学/分 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理/分 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
(1)根据上表完成下面的2×2列联表(单位:人):
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | 5 | 2 | 17 |
| 物理成绩不优秀 | 1 | 12 | 13 |
| 合计 | 6 | 14 | 20 |
附:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 参考数据 | 当Χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当Χ2>2.706时,有90%的把握判定变量A,B有关联; | |
| 当Χ2>3.841时,有95%的把握判定变量A,B有关联; | |
| 当Χ2>6.635时,有99%的把握判定变量A,B有关联. |
8.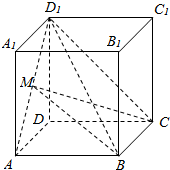 如图,已知正方体ABCD-A1B1ClD1的棱长为a,点M为线段AD1的中点.三棱锥D1-BMC的正视图面积等于( )
如图,已知正方体ABCD-A1B1ClD1的棱长为a,点M为线段AD1的中点.三棱锥D1-BMC的正视图面积等于( )
 如图,已知正方体ABCD-A1B1ClD1的棱长为a,点M为线段AD1的中点.三棱锥D1-BMC的正视图面积等于( )
如图,已知正方体ABCD-A1B1ClD1的棱长为a,点M为线段AD1的中点.三棱锥D1-BMC的正视图面积等于( )| A. | $\frac{1}{2}$a2 | B. | $\frac{1}{4}$a2 | C. | $\frac{\sqrt{2}{a}^{2}}{4}$ | D. | $\frac{\sqrt{3}{a}^{2}}{4}$ |
 如图,已知正三棱柱ABC-A1B1C1,D是AC的中点,∠α=30°,∠BDA1=90°,AB=a,求棱柱的侧面积.
如图,已知正三棱柱ABC-A1B1C1,D是AC的中点,∠α=30°,∠BDA1=90°,AB=a,求棱柱的侧面积.