题目内容
18.在区间〔-1,1〕上随机取一个数x,使sin$\frac{πx}{2}$的值介于0到$\frac{1}{2}$之间的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3π}$ | D. | $\frac{1}{6π}$ |
分析 求出0≤sin$\frac{πx}{2}$≤$\frac{1}{2}$的解集,根据几何概型的概率公式,即可求出对应的概率.
解答 解:当-1<x<1,则-$\frac{π}{2}$<$\frac{πx}{2}$<$\frac{π}{2}$,
由0≤sin$\frac{πx}{2}$≤$\frac{1}{2}$,
∴0≤$\frac{πx}{2}$≤$\frac{1}{6}$π,
即0≤x≤$\frac{1}{3}$,
则sin$\frac{πx}{2}$的值介于0到$\frac{1}{2}$之间的概率P=$\frac{\frac{1}{3}}{1-(-1)}$=$\frac{1}{6}$,
故选:B.
点评 本题主要考查几何概型的概率公式的计算,根据三角函数的性质求出对应的x的取值范围是解决本题的关键.

练习册系列答案
相关题目
8.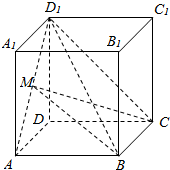 如图,已知正方体ABCD-A1B1ClD1的棱长为a,点M为线段AD1的中点.三棱锥D1-BMC的正视图面积等于( )
如图,已知正方体ABCD-A1B1ClD1的棱长为a,点M为线段AD1的中点.三棱锥D1-BMC的正视图面积等于( )
 如图,已知正方体ABCD-A1B1ClD1的棱长为a,点M为线段AD1的中点.三棱锥D1-BMC的正视图面积等于( )
如图,已知正方体ABCD-A1B1ClD1的棱长为a,点M为线段AD1的中点.三棱锥D1-BMC的正视图面积等于( )| A. | $\frac{1}{2}$a2 | B. | $\frac{1}{4}$a2 | C. | $\frac{\sqrt{2}{a}^{2}}{4}$ | D. | $\frac{\sqrt{3}{a}^{2}}{4}$ |
9.焦点分别为(-2,0),(2,0)且经过点(2,3)的双曲线的标准方程为( )
| A. | x2-$\frac{{y}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{3}-{y}^{2}=1$ | C. | y2-$\frac{{x}^{2}}{3}$=1 | D. | $\frac{{x}^{2}}{2}-\frac{{y}^{2}}{2}=1$ |
8.已知长方体的底面是正方形,且边长为2,体对角线长为2$\sqrt{5}$,则它的表面积为( )
| A. | 4(3$\sqrt{3}$+4) | B. | 8(2$\sqrt{3}$+1) | C. | 12(2$\sqrt{3}$+1) | D. | 3($\sqrt{3}$+8) |