题目内容
已知向量m=(sinA,cosA),n=( ,-1),m·n=1,且A为锐角.
,-1),m·n=1,且A为锐角.
(1)求角A的大小;
(2)求函数f(x)=cos2x+4cosAsinx(x∈R)的值域.
(1)A= .(2)函数f(x)的值域是
.(2)函数f(x)的值域是 .
.
解析试题分析:(1)由题意得m·n= sinA-cosA=1,
sinA-cosA=1,
2sin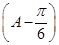 =1,sin
=1,sin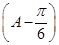 =
=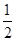 ,
,
由A为锐角得,A-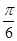 =
=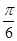 ,∴A=
,∴A= .
.
(2)由(1)知cosA=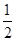 ,
,
所以f(x)=cos2x+2sinx=1-2sin2x+2sinx
=-2 2+
2+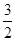 .
.
因为x∈R,所以sinx∈[-1,1],
因此,当sinx=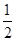 时,f(x)有最大值
时,f(x)有最大值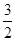 ,
,
当sinx=-1时,f(x)有最小值-3,
所以所求函数f(x)的值域是 .
.
考点:平面向量的坐标运算,和差倍半的三角函数,三角函数的图象和性质,二次函数的图象和性质。
点评:中档题,本题较为典型,即首先通过平面向量的坐标运算,得到三角函数式,利用和差倍半的三角函数公式,将三角函数式“化一”,进一步研究函数的图像和性质。本题利用换元思想,将问题转化成二次函数在闭区间的最值问题,使问题更具综合性。

练习册系列答案
相关题目
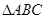 中,
中, ,
, ,
, .
. 的大小;
的大小; 的取值范围.
的取值范围.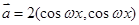 ,
,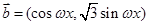 (其中
(其中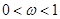 ),函数
),函数 ,若直线
,若直线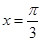 是函数
是函数 图象的一条对称轴.
图象的一条对称轴.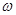 的值;
的值;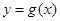 的图象是由
的图象是由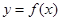 的图象的各点的横坐标伸长到原来的2倍,然后再向左平移
的图象的各点的横坐标伸长到原来的2倍,然后再向左平移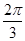 个单位长度得到,求
个单位长度得到,求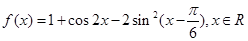 .
. 的最小正周期和对称中心;
的最小正周期和对称中心;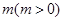 个单位后所得到的图像关于
个单位后所得到的图像关于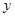 轴对称,求实数
轴对称,求实数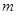 的最小值.
的最小值.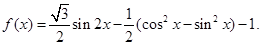
 的最小值和最小正周期;
的最小值和最小正周期;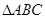 的内角
的内角 、
、 、
、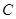 的对边分别为
的对边分别为 、
、 、
、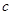 且
且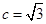 ,
,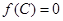 ,若向量
,若向量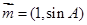 与向量
与向量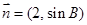 共线,求
共线,求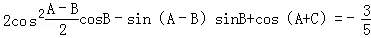
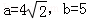 ,求向量
,求向量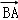 在
在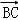 方向上的投影.
方向上的投影. .
. 的最小值和最小正周期;
的最小值和最小正周期; 的内角
的内角 的对边分别为
的对边分别为 且
且 ,
, ,若
,若 ,求
,求 的值。
的值。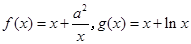 ,其中
,其中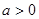 .
.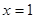 是函数
是函数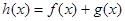 的极值点,求实数
的极值点,求实数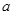 的值;
的值;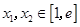 (
(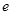 为自然对数的底数)都有
为自然对数的底数)都有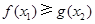 成立,求实数
成立,求实数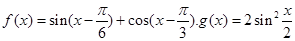 。
。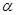 是第一象限角,且
是第一象限角,且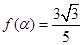 。求
。求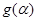 的值;
的值;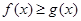 成立的x的取值集合。
成立的x的取值集合。