题目内容
【题目】已知f(x)＝
，x∈(－2，2)．
(1) 判断f(x)的奇偶性并说明理由；
(2) 求证：函数f(x)在(－2，2)上是增函数；
(3) 若f(2＋a)＋f(1－2a)>0，求实数a的取值范围．
【答案】(1) 见解析：(2) 见解析：(3) a∈
.
【解析】试题分析：（1）定义域 关于原点对称，同时满足f(x)=-f(-2)，所以是奇函数。（2）由定义法证明函数的单调性，按假设，作差，变形，判断，下结论过程完成。（3）由奇函数，原不等式变形为f(2＋a)>－f(1－2a)＝f(2a－1)，再由函数单调性及定义域可知
，解不等式组可解。
试题解析：(1) 解：∵ f(－x)＝
＝－
＝－f(x)，∴ f(x)是奇函数．
(2) 证明：设x1，x2为区间(－2，2)上的任意两个值，且x1<x2，则f(x1)－f(x2)＝
－
＝
，
因为－2<x1<x2<2，所以x2－x1>0，x1x2－4<0，所以f(x1)－f(x2)<0，f(x1)<f(x2)，
所以函数f(x)在(－2，2)上是增函数．
(3) 解：因为f(x)为奇函数，所以由f(2＋a)＋f(1－2a)>0得，f(2＋a)>－f(1－2a)＝f(2a－1)，
因为函数f(x)在(－2，2)上是增函数，
所以即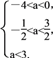
故a∈
.
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
