Question

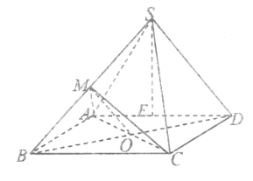
【题目】如图，已知四棱锥，底面是边长为的菱形，，侧面为正三角形，侧面底面，为侧棱的中点，为线段的中点

（Ⅰ）求证：平面；

（Ⅱ）求证：；

（Ⅲ）求三棱锥的体积

Answer 1

【答案】（Ⅰ）见解析（Ⅱ）见解析（Ⅲ）

【解析】

（Ⅰ）连接，交于点；根据三角形中位线可证得；由线面平行判定定理可证得结论；（Ⅱ）由等腰三角形三线合一可知；由面面垂直的性质可知平面；根据线面垂直性质可证得结论；（Ⅲ）利用体积桥的方式将所求三棱锥体积转化为；根据已知长度和角度关系分别求得四边形面积和高，代入得到结果.

（Ⅰ）证明：连接，交于点

四边形为菱形 为中点

又为中点

平面，平面 平面

（Ⅱ）为正三角形，为中点

平面平面，平面平面，平面

平面，又平面

（Ⅲ）为中点

又，

，

由（Ⅱ）知，