题目内容
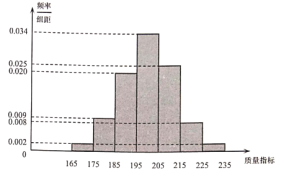
【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取100件产品作为样本称出它们的质量(单位:毫克),质量值落在![]() 的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
产品质量/毫克 | 频数 |
| 3 |
| 9 |
| 19 |
| 35 |
| 22 |
| 7 |
| 5 |
(1)由以上统计数据完成下面![]() 列联表,能否在犯错误的概率不超过0.15的前提下认为产品的包装合格与两条自动包装流水线的选择有关?
列联表,能否在犯错误的概率不超过0.15的前提下认为产品的包装合格与两条自动包装流水线的选择有关?
甲流水线 | 乙流水线 | 总计 | |
合格品 | |||
不合格品 | |||
总计 |
附表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,
,![]() )
)
(2)按照以往经验,在每小时次品数超过180件时,产品的次品率会大幅度增加,为检测公司的生产能力,同时尽可能控制不合格品总量,公司工程师抽取几组一小时生产产品数据进行次品情况检查分析,在![]() (单位:百件)件产品中,得到次品数量
(单位:百件)件产品中,得到次品数量![]() (单位:件)的情况汇总如下表所示:
(单位:件)的情况汇总如下表所示:
| 0.5 | 2 | 3.5 | 4 | 5 |
| 2 | 14 | 24 | 35 | 40 |
根据公司规定,在一小时内不允许次品数超过180件,请通过计算分析,按照公司的现有生产技术设备情况,判断可否安排一小时生产2000件的任务?
(参考公式:用最小二乘法求线性回方程![]() 的系数公式
的系数公式

 ;
;![]() )
)
【答案】(1)详见解析;(2)可以安排一小时生产2000件的任务.
【解析】
(1)根据题干补全列联表,由卡方公式计算得到卡方值,从而进行判断;(2)根据公式得到线性回归方程,将x=20百件时代入方程,进行判断可得到结果.
(1)由乙流水线样本的频率分布直方图可知,合格品的个数为![]() ,
,
所以,![]() 列联表是:
列联表是:
甲流水线 | 乙流水线 | 总计 | |
合格品 | 92 | 96 | 188 |
不合格品 | 8 | 4 | 12 |
总计 | 100 | 100 | 200 |
所以![]()
![]() .
.
所以,在犯错误的概率不超过0.15的前提下,不能认为产品的包装合格与两条自动包装流水线的选择有关.
(2)由已知可得:![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
由回归直线的系数公式,
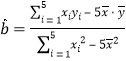
![]() .
.
![]() .
.
所以![]() .
.
当![]() (百件)时,
(百件)时,![]() ,符合有关要求.
,符合有关要求.
所以按照公司的现有生产技术设备情况,可以安排一小时生产2000件的任务.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案