题目内容
【题目】已知函数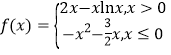 ,若方程
,若方程![]() (
(![]() 为常数)有两个不相等的根,则实数
为常数)有两个不相等的根,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】D
【解析】
求出当x>0时,函数的导数,研究函数的极值和图象,作出函数f(x)的图象,由数形结合进行求解即可.
当x>0时,函数f′(x)=2﹣(lnx+1)=1﹣lnx,
由f′(x)>0得1﹣lnx>0得lnx<1,得0<x<e,
由f′(x)<0得1﹣lnx<0得lnx>1,得x>e,当x值趋向于正无穷大时,y值也趋向于负无穷大,即当x=e时,函数f(x)取得极大值,
极大值为f(e)=2e﹣elne=2e﹣e=e,
当x≤0时,f(x)=﹣x2﹣![]() x=﹣(x+
x=﹣(x+![]() )2+
)2+![]() ,是二次函数,在轴处取得最大值
,是二次函数,在轴处取得最大值![]() ,
,
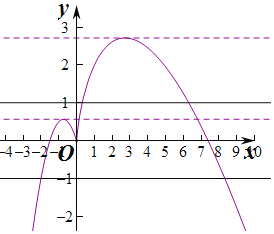
作出函数f(x)的图象如图:
要使f(x)=a(a为常数)有两个不相等的实根,
则a<0或![]() <a<e,
<a<e,
即实数a的取值范围是(﹣∞,0)∪![]() ,
,
故选:D.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
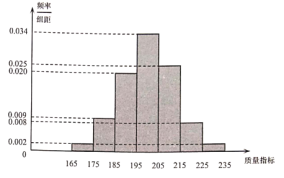
优翼小帮手同步口算系列答案【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取100件产品作为样本称出它们的质量(单位:毫克),质量值落在![]() 的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
产品质量/毫克 | 频数 |
| 3 |
| 9 |
| 19 |
| 35 |
| 22 |
| 7 |
| 5 |
(1)由以上统计数据完成下面![]() 列联表,能否在犯错误的概率不超过0.15的前提下认为产品的包装合格与两条自动包装流水线的选择有关?
列联表,能否在犯错误的概率不超过0.15的前提下认为产品的包装合格与两条自动包装流水线的选择有关?
甲流水线 | 乙流水线 | 总计 | |
合格品 | |||
不合格品 | |||
总计 |
附表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,
,![]() )
)
(2)按照以往经验,在每小时次品数超过180件时,产品的次品率会大幅度增加,为检测公司的生产能力,同时尽可能控制不合格品总量,公司工程师抽取几组一小时生产产品数据进行次品情况检查分析,在![]() (单位:百件)件产品中,得到次品数量
(单位:百件)件产品中,得到次品数量![]() (单位:件)的情况汇总如下表所示:
(单位:件)的情况汇总如下表所示:
| 0.5 | 2 | 3.5 | 4 | 5 |
| 2 | 14 | 24 | 35 | 40 |
根据公司规定,在一小时内不允许次品数超过180件,请通过计算分析,按照公司的现有生产技术设备情况,判断可否安排一小时生产2000件的任务?
(参考公式:用最小二乘法求线性回方程![]() 的系数公式
的系数公式
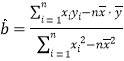
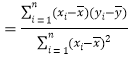 ;
;![]() )
)
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:万元)的影响.对近六年的年宣传费
(单位:万元)的影响.对近六年的年宣传费![]() 和年销售量
和年销售量![]() (
(![]() )的数据作了初步统计,得到如下数据:
)的数据作了初步统计,得到如下数据:
年份 |
|
|
|
|
|
|
年宣传费 |
|
|
|
|
|
|
年销售量 |
|
|
|
|
|
|
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() (
(![]() ).对上述数据作了初步处理,得到相关的值如表:
).对上述数据作了初步处理,得到相关的值如表:
|
|
|
|
|
|
|
|
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)已知这种产品的年利润![]() 与
与![]() ,
,![]() 的关系为
的关系为![]() 若想在
若想在![]() 年达到年利润最大,请预测
年达到年利润最大,请预测![]() 年的宣传费用是多少万元?
年的宣传费用是多少万元?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]()