题目内容
【题目】已知抛物线x2=4y,圆C:x2+(y﹣2)2=4,点M(x0 , y0),(x0>0,y0>4)为抛物线上的动点,过点M的圆C的两切线,设其斜率分别为k1 , k2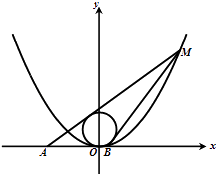
(Ⅰ)求证:k1+k2= ![]() ,k1k2=
,k1k2= ![]() .
.
(Ⅱ)求过点M的圆的两切线与x轴围成的三角形面积S的最小值.
【答案】解:(I)证明:设切线方程y﹣y0=k(x﹣x0),即kx﹣y+y0﹣kx0=0, 切线与x轴交为( ![]() ,0),圆心到直线的距离d=
,0),圆心到直线的距离d= ![]() =2
=2
整理得: ![]()
由两切线的斜率分别为k1 , k2
则k1+k2= ![]() ,k1k2=
,k1k2= ![]() ,
,
(Ⅱ)S= ![]() |(
|( ![]() )﹣(
)﹣( ![]() )|y0
)|y0
= ![]() y02
y02 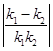
= ![]() y02
y02 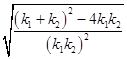
= ![]() y02
y02 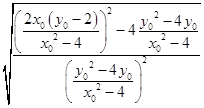
= 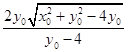
= ![]()
=2[ ![]() +(y0﹣4)+8]
+(y0﹣4)+8]
≥2(2 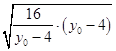 +8)
+8)
=32.
当且仅当 ![]() =y0﹣4,即y0=8时取等号.
=y0﹣4,即y0=8时取等号.
故两切线与x轴围成的三角形面积S的最小值为32
【解析】(I)设切线:y﹣y0=k(x﹣x0),切线与x轴交于点( ![]() ,0),圆心到切线的距离d=
,0),圆心到切线的距离d= ![]() =2,结合韦达定理,可得k1+k2=
=2,结合韦达定理,可得k1+k2= ![]() ,k1k2=
,k1k2= ![]() .(Ⅱ)求出过点M的圆的两切线与x轴围成的三角形面积S的表达式,由基本不等式可求出两切线与x轴围成的三角形面积S的最小值.
.(Ⅱ)求出过点M的圆的两切线与x轴围成的三角形面积S的表达式,由基本不等式可求出两切线与x轴围成的三角形面积S的最小值.

 阅读快车系列答案
阅读快车系列答案【题目】某公司为了解用户对其产品的满意度,从某地区随机调查了100个用户,得到用户对产品的满意度评分频率分布表如下:
组别 | 分组 | 频数 | 频率 |
第一组 | (50,60] | 10 | 0.1 |
第二组 | (60,70] | 20 | 0.2 |
第三组 | (70,80] | 40 | 0.4 |
第四组 | (80,90] | 25 | 0.25 |
第五组 | (90,100) | 5 | 0.05 |
合计 | 100 | 1 |
(1)根据上面的频率分布表,估计该地区用户对产品的满意度评分超过70分的概率;
(2)请由频率分布表中数据计算众数、中位数,平均数,根据样本估计总体的思想,若平均分低于75分,视为不满意.判断该地区用户对产品是否满意?