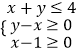题目内容
【题目】已知A、B是函数y=f（x），x∈[a，b]图象的两个端点，M（x，y）是f（x）上任意一点，过M（x，y）作MN⊥x轴交直线AB于N，若不等式|MN|≤k恒成立，则称函数f（x）在[a，b]上“k阶线性近似”．
（1）若f（x）=x+ 
，x∈[ 
，2]，证明：f（x）在[ ，2]上“ 阶线性近似”；
（2）若f（x）=x2在[﹣1，2]上“k阶线性近似”，求实数k的最小值．
【答案】
（1）证明：若f（x）=x+ 
，x∈[ 
，2]，则A（ ， 
）、B（2， ），
故直线AB的方程为：y= ，
则由|MN|= ﹣（x+ ），
∴|MN|∈[0， ]，
故|MN|≤ ，
故f（x）在[ ，2]上“ 阶线性近似”
（2）解：由MN⊥x交直线AB于N，得 N 和M的横坐标相同．
对于区间[﹣1，2]上的函数f（x）=x2 ，A（﹣1，1）、B（2，4），
则直线AB的方程为：y=x+2，
则有|MN|=x+2﹣x2=﹣（x﹣ ）2+ 
，
∴|MN|∈[0， ]．
再由|MN|≤k恒成立，可得 k≥ 
．
故实数k的最小值为 ．
【解析】（1）根据对勾函数的图象和性质，得到f（x）=x+ 
，x∈[ 
，2]，满足|MN|≤ ，进而得到答案．（2）由已知可得 N和M的横坐标相同，根据|MN|=x+2﹣x2=﹣（x﹣ ）2+ 
及x∈[﹣1，2]，求出|MN|的范围，再由|MN|≤k恒成立，求得k的取值范围．
【考点精析】认真审题，首先需要了解函数的图象(函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值)．
练习册系列答案
相关题目
