题目内容
(12分)已知函数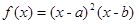 (
(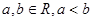 ).
).
①当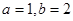 时,求曲线
时,求曲线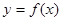 在点
在点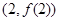 处的切线方程;
处的切线方程;
②设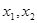 是
是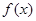 的两个极值点,
的两个极值点,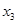 是
是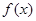 的一个零点
的一个零点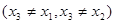 .证明:存在实数
.证明:存在实数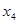 ,使得
,使得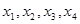 按某种顺序排列后构成等差数列,并求
按某种顺序排列后构成等差数列,并求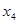 .
.
① .②存在实数
.②存在实数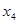 满足题意,且
满足题意,且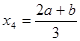 .
.
解析试题分析:(1)将a,b的值代入后对函数f(x)进行求导,根据导数的几何意义即函数在某点的导数值等于该点的切线的斜率,可得答案.
(2)对函数f(x)求导,令导函数等于0解出x的值,然后根据x3是f(x)的一个零点可得到x3=b,然后根据等差数列的性质可得到答案.
解:①当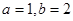 时,
时, ,故
,故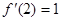 ,又
,又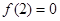 ,
,
所以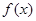 点
点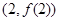 处的切线方程为:
处的切线方程为: .
.
②证明:因为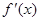 =
= ,由于
,由于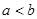 ,故
,故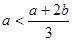 ,
,
所以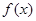 的两个极值点为
的两个极值点为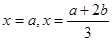 ,不妨设
,不妨设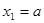 ,
,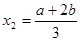 ,
,
因为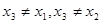 ,且
,且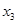 是
是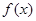 的一个零点,故
的一个零点,故 ,
,
由于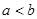 ,故
,故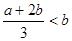 ,故
,故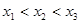 ,又
,又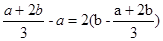 ,
,
故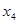 =
= ,此时
,此时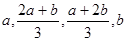 依次成等差数列,
依次成等差数列,
所以存在实数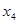 满足题意,且
满足题意,且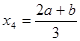 .
.
考点:本题主要考查函数的极值概念、导数运算法则、切线方程、导线应用、等差数列等基础知识,同时考查抽象概括、推理论证能力和创新意识.
点评:对于导数在研究函数中的运用问题,对于导数的几何意义是考试的必考的一个知识点,要引起重视,同时对于极值点的导数为零是该点为极值点的必要不充分条件。

练习册系列答案
相关题目
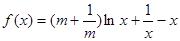 ,其中常数
,其中常数 .
.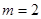 时,求函数
时,求函数 的极大值;
的极大值;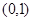 上的单调性;
上的单调性; 时,曲线
时,曲线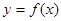 上总存在相异两点
上总存在相异两点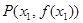 ,
,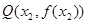 ,使得曲线
,使得曲线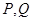 处的切线互相平行,求
处的切线互相平行,求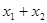 的取值范围.
的取值范围. - 2的极值.
- 2的极值.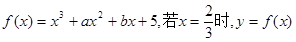 有极值,且曲线
有极值,且曲线 处的切线斜率为3.
处的切线斜率为3. 的解析式;
的解析式; 在
在 上的最大值和最小值.
上的最大值和最小值.
 是
是 的一个极值点.
的一个极值点. 时,
时, 恒成立,求
恒成立,求 的取值范围。
的取值范围。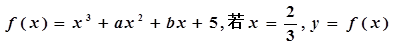 有极值,且曲线
有极值,且曲线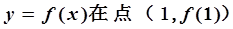 处的切线斜率为3.
处的切线斜率为3.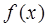 的解析式;
的解析式;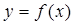 在[-4,1]上的最大值和最小值。
在[-4,1]上的最大值和最小值。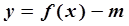 有三个零点,求实数
有三个零点,求实数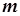 的取值范围.
的取值范围.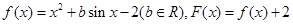 ,且对于任意实数
,且对于任意实数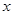 ,恒有
,恒有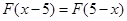 .
. 的解析式;
的解析式;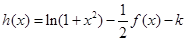 有几个零点?
有几个零点?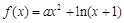 .
.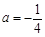 时,求函数
时,求函数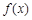 的单调区间;
的单调区间;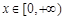 时,函数
时,函数 图象上的点都在
图象上的点都在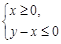 所表示的平面区域内,求实数a的取值范围.
所表示的平面区域内,求实数a的取值范围.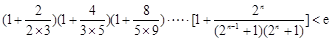 (其中
(其中 ,e是自然对数的底数).
,e是自然对数的底数).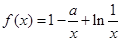 (
( 为实常数).
为实常数).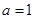 时,求函数
时,求函数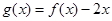 的单调区间;
的单调区间; 在区间
在区间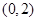 上无极值,求
上无极值,求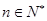 且
且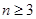 ,求证:
,求证: 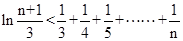 .
.