题目内容
已知等差数列 满足
满足 .
.
(1)求 的通项公式;
的通项公式;
(2)求 的前
的前 项和
项和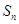 ;
;
(3)若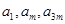 成等比数列,求
成等比数列,求 的值.
的值.
(1)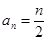 (2)
(2)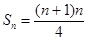 (3)
(3)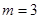
解析试题分析:
(1)法一:根据数列是等差数列,采用特殊值带入 ,求出首项和公差,得通项公式;法二:根据等差数列的通项公式展开
,求出首项和公差,得通项公式;法二:根据等差数列的通项公式展开 的左侧,则其左侧含有
的左侧,则其左侧含有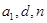 ,根据等式相等关系,可得
,根据等式相等关系,可得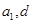 ,从而得到通项公式.
,从而得到通项公式.
(2)利用等差数列前 项和公式以及(1)中的结论直接求即可.
项和公式以及(1)中的结论直接求即可.
(3)根据(1)中结论,以及等比中项可解该问.
(1)解法一:设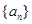 的公差为
的公差为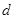 , 因为
, 因为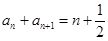 ,
,
所以有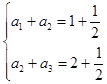 ,两式相减得到,
,两式相减得到,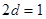 ,即
,即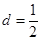
代入得到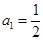
所以
解法二:设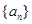 的公差为
的公差为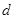 ,
,
则
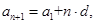
所以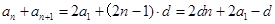
所以有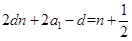 对
对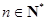 成立,
成立,
所以有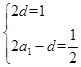 ,解得
,解得
所以
(2) 因为 所以
所以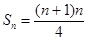
(3)因为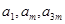 成等比数列,所以
成等比数列,所以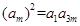
即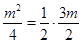
解得
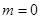 (舍掉) ,所以
(舍掉) ,所以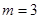 …
…
考点:等差数列通项公式,前 项和公式,等比中项.
项和公式,等比中项.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
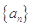 的首项
的首项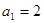 ,且对任意
,且对任意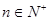 都有
都有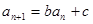 (其中
(其中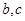 为常数).
为常数). 为等差数列,且
为等差数列,且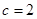 ,求
,求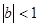 ,从数列
,从数列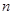 项和
项和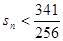 成立的
成立的 的三个内角
的三个内角 成等差数列,求证:
成等差数列,求证:
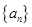 的首项
的首项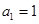 ,公差
,公差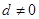 ,等比数列
,等比数列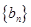 满足
满足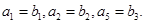
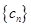 对任意
对任意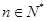 均有
均有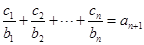 ,求数列
,求数列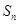 .
.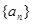 的各项都为正数,
的各项都为正数, 。
。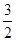 的等差数列,求
的等差数列,求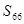 ;
;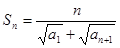 ,求证:数列
,求证:数列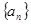 中,
中,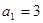 ,公差为
,公差为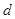 ,其前
,其前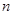 项和为
项和为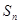 ,在等比数列
,在等比数列 中,
中,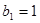 ,公比为
,公比为 ,且
,且 ,
,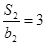 .
.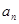 与
与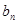 ;
;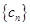 满足
满足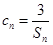 ,求
,求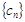 的前
的前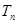 .
.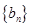 中的
中的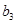 、
、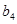 、
、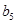 .
.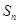 ,求证:数列
,求证:数列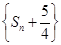 是等比数列.
是等比数列.