题目内容
已知数列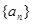 的各项都为正数,
的各项都为正数, 。
。
(1)若数列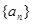 是首项为1,公差为
是首项为1,公差为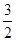 的等差数列,求
的等差数列,求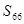 ;
;
(2)若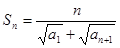 ,求证:数列
,求证:数列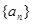 是等差数列.
是等差数列.
(1)6, (2)详见解析.
解析试题分析:(1)数列求和,关键分析通项特征.本题通项 因此求和可用裂项相消法. 因为
因此求和可用裂项相消法. 因为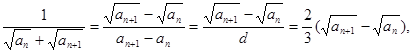 所以
所以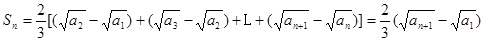
从而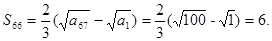 (2)证明数列为等差数列,一般方法为定义法.由条件
(2)证明数列为等差数列,一般方法为定义法.由条件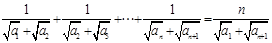 可得
可得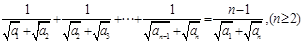 两式相减得:
两式相减得: 化简得:
化简得: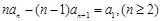 ,这是数列的递推关系,因此再令
,这是数列的递推关系,因此再令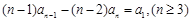 两式相减得:
两式相减得: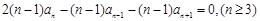 即
即 ,由
,由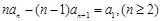 得
得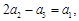 所以
所以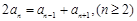 即
即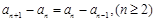 ,因此数列
,因此数列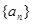 是等差数列.
是等差数列.
(1)由题意得:
因为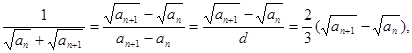
所以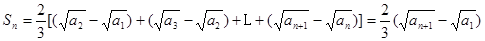
从而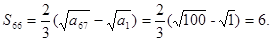
(2) 由题意得: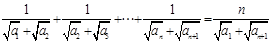 ,所以
,所以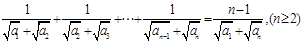 两式相减得:
两式相减得: ,
,
化简得: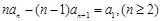 ,因此
,因此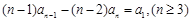 两式相减得:
两式相减得: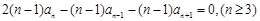 即
即 ,由
,由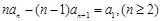 得
得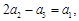 所以
所以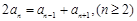 即
即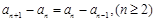 ,因此数列
,因此数列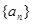 是等差数列.
是等差数列.
考点:列项相消法求和,等差数列证明

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
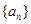 中,
中,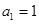 ,对于任意
,对于任意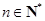 ,都有
,都有 ,
,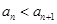 . 设
. 设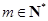 , 记使得
, 记使得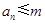 成立的
成立的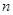 的最大值为
的最大值为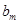 .
.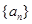 为1,3,5,7,
为1,3,5,7,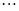 ,写出
,写出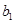 ,
,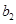 ,
,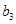 的值;
的值;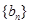 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列 ,
,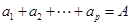 ,求
,求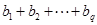 的值.(用
的值.(用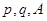 表示)
表示) 为等差数列
为等差数列 的前
的前 项和,
项和,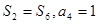 ,求
,求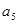 ;
; ,求首项
,求首项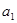 和公比
和公比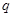
 满足
满足 .
. 项和
项和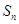 ;
;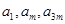 成等比数列,求
成等比数列,求 的值.
的值.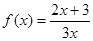 , 数列
, 数列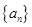 满足
满足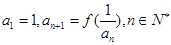 .
.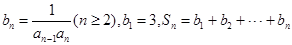 ,若
,若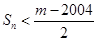 对一切
对一切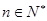 成立,求最小正整数m.
成立,求最小正整数m.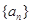 的前n项和为
的前n项和为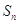 ,存在常数A,B,C,使得
,存在常数A,B,C,使得 对任意正整数n都成立.
对任意正整数n都成立.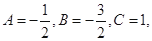 设
设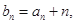 数列
数列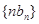 的前n项和为
的前n项和为 ,求
,求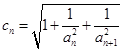 数列
数列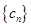 的前2014项和为P,求不超过P的最大整数的值.
的前2014项和为P,求不超过P的最大整数的值. 为等比数列,其前n项和为
为等比数列,其前n项和为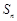 ,且满足
,且满足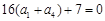 ,
,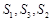 成等差数列.
成等差数列.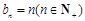 ,记
,记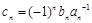 ,求数列
,求数列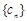 前n项和
前n项和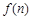 .
.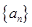 的各项均为正数,且
的各项均为正数,且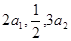 成等差数列,
成等差数列, 成等比数列.
成等比数列. ,记
,记 ,
,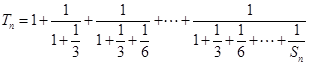 ,求证:
,求证: