题目内容
已知数列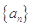 的首项
的首项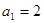 ,且对任意
,且对任意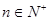 都有
都有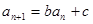 (其中
(其中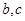 为常数).
为常数).
(1)若数列 为等差数列,且
为等差数列,且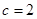 ,求
,求 的通项公式.
的通项公式.
(2)若数列 是等比数列,且
是等比数列,且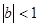 ,从数列
,从数列 中任意取出相邻的三项,均能按某种顺序排成等差数列,求
中任意取出相邻的三项,均能按某种顺序排成等差数列,求 的前
的前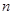 项和
项和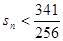 成立的
成立的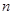 的取值的集合.
的取值的集合.
(1)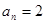 或
或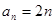 ;(2){2,4,6,8} .
;(2){2,4,6,8} .
解析试题分析:(1)对实数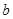 分类讨论,①
分类讨论,①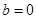 ,
,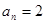 ;②
;②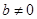 时,根据等差数列的定义,可知
时,根据等差数列的定义,可知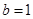 ,公差
,公差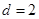 ,则
,则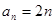 ;(2)若数列
;(2)若数列 为等比数列,则
为等比数列,则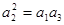 ,即
,即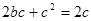 ,因此
,因此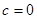 (注意
(注意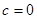 是容易漏掉的)或
是容易漏掉的)或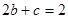 , 在这
, 在这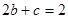 情况下,可得
情况下,可得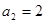 ,故
,故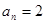 不满足
不满足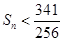 ,因此只有
,因此只有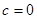 满足条件,由任相邻的三项均能按某种顺序排成等差数列,可分为以下三种情况:①
满足条件,由任相邻的三项均能按某种顺序排成等差数列,可分为以下三种情况:①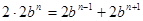 ;②
;②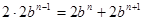 ;③
;③ ,分别求出
,分别求出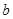 看是否满足条件,由满足条件的
看是否满足条件,由满足条件的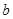 结合
结合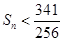 确定
确定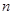 的取值的个数.
的取值的个数.
(1)当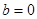 时,
时,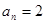 符合题意,
符合题意,
当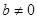 时,由于数列
时,由于数列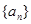 是等差数列且
是等差数列且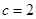 ,所以
,所以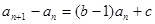 为常数,故
为常数,故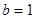 ,得
,得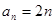 ,
,
所以,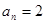 或
或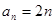 .(6分)(只求得一个得3分)
.(6分)(只求得一个得3分)
(2)由数列 为等比数列,所以
为等比数列,所以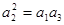 得
得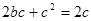
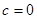 或
或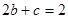 , (8分)
, (8分)
若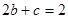 得
得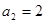 ,故
,故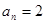 不满足
不满足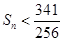
所以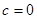 ,得
,得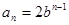 .
.
由任相邻的三项均能按某种顺序排成等差数列,即
若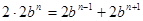 得
得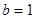 (舍).
(舍).
若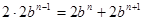 得
得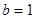 (舍)或
(舍)或 (舍),
(舍),
若 得
得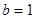 舍或
舍或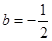 ,
,
故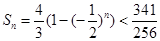 得
得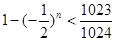
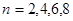 即所求值的集合为{2,4,6,8} (13分)
即所求值的集合为{2,4,6,8} (13分)
考点:等差数列、等比数列的性质.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
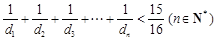 .
. 中,
中,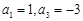 .
.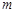 项和
项和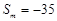 ,求
,求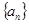 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列, 表示
表示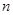 项和.
项和. 及
及 是首项为2的等比数列,公比
是首项为2的等比数列,公比 满足
满足 ,求
,求 .
. 满足:
满足: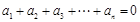 且
且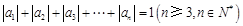 ,则称数列
,则称数列 阶“归化数列”.
阶“归化数列”.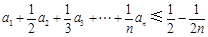 .
.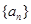 的各项均为正数,记
的各项均为正数,记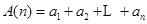 ,
,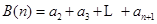 ,
,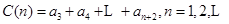 .
.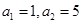 ,且对任意
,且对任意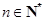 ,三个数
,三个数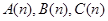 组成等差数列,求数列
组成等差数列,求数列 的等比数列的充分必要条件是:对任意
的等比数列的充分必要条件是:对任意 满足
满足 .
. 项和
项和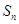 ;
;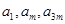 成等比数列,求
成等比数列,求 的值.
的值.